Academic textbooks are silent about T-handles making spectacular somersaults in space, with no forces acting, except of the old fashioned and mysterious “force of inertia”. And why is it so? My answer is simple: because of inadequate education. Inadequately trained are physicists and mathematicians. Therefore, of course, engineers as well. Not just inadequately educated. Lazy they are as well. Since they can learn from the available sources. But they do not want. They prefer going the parties and pubs, and watching movies. Learning about elliptic functions is too much of a trouble for them. It was not so some one hundred years ago. But it is very bad now, when what counts in science are “impact factor points” rather than knowledge. Papers are written nowadays not in order to share research results. They are written for providing “impact factor points”.
“The impact factor (IF) is a measure of the frequency with which the average article in a journal has been cited in a particular year. It is used to measure the importance or rank of a journal by calculating the times it’s articles are cited.”
10 simple strategies to increase the impact factor of your publication
“Impact factors are heavily criticized as measures of scientific quality. However, they still dominate every discussion about scientific excellence. They are still used to select candidates for positions as PhD student, postdoc and academic staff, to promote professors and to select grant proposals for funding. As a consequence, researchers tend to adapt their publication strategy to avoid negative impact on their careers. Until alternative methods to measure excellence are established, young researchers have to learn the “rules of the game”.”
The effect we are discussing, the so called Dzhanibekov effect, has been discovered by chance by the Russian cosmonaut and scientist V. A. Dzhanibekov in 1985.

The discovery apparently has been kept in secrecy for 10 years. But I think that the Americans have learned about this “secret” almost immediately and they charged their scientists, experts in gravity effects, with the task of checking if the effect is important for the Defense of the Country.
I think that the experts quickly came to the conclusion that they do not see anything of a practical value here, there are no national security threats from nuts freely flipping in space, and therefore they decided to let the mathematicians to publish a paper on the subject:
Mark S. Ashbaugh, Carmen C. Chicone and Richard H. Cushman, “The Twisting Tennis Racket“. Journal of Dynamics and Differential Equations. 3 (1): 67–85 (1991)
Two of the authors, Aschbaugh and Chicone, were mathematicians from the University of Missouri, the third one, Cushman, a mathematician from Utrecht. They wrote in their paper that W. Burke from the University of California at Santa Cruz has shown to Cushman the effect. The effect they described consisted of:
The classical treatments of the dynamics of a tennis racket about its intermediate axis fail to describe a remarkable aspect of its motion which is revealed in the following experiment. Mark the faces of the racket so that they can be distinguished. Call one rough and the other smooth. Hold the racket horizontally by its handle with the smooth face up. Toss the racket into the air attempting to make it rotate about the intermediate axis (namely, the axis in the plane of the face which is perpendicular to the handle). After one rotation, catch the racket by the handle. The rough face will almost always be up! In other words, the racket typically makes a half-
twist about its handle.
It is rather lame when compared to the effect with a flipping T-handle that has been observed in space:
Burke was a physicist working on gravity. The three mathematicians together managed to conclude that strange behavior is to be expected. But they were not able to solve the problem completely. Cushmann tried to solve the problem later on. In 2000 he has published a set of lectures entitled “No polar coordinates“, where he admitted: “I am not a master of Weierstrass’ theory of elliptic functions, so I won’t do this integral. But Whittaker [42] is and he does it.” Strange, a mathematician, and he does not know how to integrate, and does not even want to know.
But we want to know, we want to tame the flipping T-handle. Domesticated, tamed animals are useful.

In the last post, Standing on the shoulders of giants, I used the ideas from the paper by Ramses van Zon, Jeremy Schofield, “Numerical implementation of the exact dynamics of free rigid bodies“, J. Comput. Phys. 225, 145-164 (2007), and we came to the point where we have represented the attitude matrix ![]() as the product:
as the product:
(1) ![]()
where
(2) 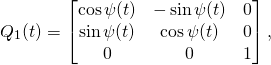
(3) 
(4) ![]()
(5) ![]()
and ![]() is the solution of the Euler equations (this time we write them in terms of angular momentum rather than angular velocity):
is the solution of the Euler equations (this time we write them in terms of angular momentum rather than angular velocity):
(6) 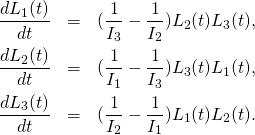
The task is now to derive the differential equation for ![]() knowing that
knowing that ![]() satisfies the equation
satisfies the equation
(7) ![]()
where
![Rendered by QuickLaTeX.com \[W(t)=\begin{bmatrix}0&-\Omega_3(t)&\Omega_2(t)\\\Omega_3(t)&0&-\Omega_1(t)\\-\Omega_2(t)&\Omega_1(t)&0\end{bmatrix}=\begin{bmatrix}0&-\frac{L_3(t)}{I_3}&\frac{L_2(t)}{I_2}\\\frac{L_3(t)}{I_3}&0&-\frac{L_1(t)}{I_1}\\-\frac{L_2(t)}{I_2}&\frac{L_1(t)}{I_1}&0\end{bmatrix}.\]](http://arkadiusz-jadczyk.eu/blog/wp-content/ql-cache/quicklatex.com-ccf6476a5a9e964d7c6b573536195187_l3.png)
Getting the differential equation for ![]() is now a purely mechanical task. Therefore I will simply show the end result, and then show the REDUCE code that verifies this result. The result is:
is now a purely mechanical task. Therefore I will simply show the end result, and then show the REDUCE code that verifies this result. The result is:
(8) ![]()
And here is the REDUCE code. It has two parts. Here we use the first part, but at the end of this post we are also using the second part:
OPERATOR Q0,Q1,W,psi,L1,L2,L3,L,Lp;
Lp(t):=sqrt(L1(t)**2+L2(t)**2);
% L:=sqrt(L1(t)**2+L2(t)**2+L3(t)**2);
Q0:=MAT(
(L1(t)*L3(t)/(L*Lp(t)),L2(t)*L3(t)/(L*Lp(t)),-Lp(t)/L),
(-L2(t)/Lp(t),L1(t)/Lp(t),0),
(L1(t)/L,L2(t)/L,L3(t)/L));
Q1:=MAT((cos(psi(t)),-sin(psi(t)),0),(sin(psi(t)),cos(psi(t)),0),(0,0,1));
W:=MAT( (0,-L3(t)/I3,L2(t)/I2),(L3(t)/I3,0,-L1(t)/I1),(-L2(t)/I2,L1(t)/I1,0));
FOR ALL t LET L3(t)**2=L**2-L1(t)**2-L2(t)**2;
FOR ALL X LET COS X**2=1-(SIN X)**2;
FOR ALL t let
DF(L1(t),t)=(1/I3-1/I2)*L2(t)*L3(t),
DF(L2(t),t)=(1/I1-1/I3)*L3(t)*L1(t),
DF(L3(t),t)=(1/I2-1/I1)*L1(t)*L2(t);
Q:=Q1*Q0;
eq1:=(Q1*Q0*W-Q1*DF(Q0,t))*Tp(Q0);
% Here we get the same d psi/dt from four entries of the matrix
dpsi1:=eq1(1,1)/(-sin(psi(t)));
dpsi2:=eq1(1,2)/(-cos(psi(t)));
dpsi3:=eq1(2,1)/(cos(psi(t)));
dpsi4:=eq1(2,2)/(-sin(psi(t)));
Q1*Q0*MAT((L1(t)),(L2(t)),(L3(t)));
FOR ALL t LET DF(psi(t),t)=dpsi1;
%And here we check that we have the right equation:
DF(Q,t)-Q*W;
% This is the second part, where we substitute expressions for L1,L2,L3 and verify
A1:=L*sqrt(I1*(d*I3-1)/(I3-I1));
A2:=L*sqrt(I2*(d*I3-1)/(I3-I2));
A3:=L*sqrt(I3*(1 - d*I1)/(I3 - I1));
L1(t):=A1*cn(t);
L2(t):=A2*sn(t);
L3(t):=A3*dn(t);
FOR ALL t LET cn(t)^2=1-sn(t)^2;
dpsi1;
c1:=1/I3;
c2:=1/I1-1/I3;
C3:=(I3*(I2-I1))/(I1*(I3-I2));
dpsi1-L*(c1+c2/(1+c3*sn(t)^2));
END;
Next thing is to use our formulas for the solutions of the Euler equations ![]() – see Solving Euler’s equations. Here we adapt these formulas so that they give the solution for
– see Solving Euler’s equations. Here we adapt these formulas so that they give the solution for ![]() rather than for
rather than for ![]() :
:
(9) 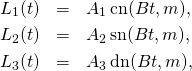
(10) 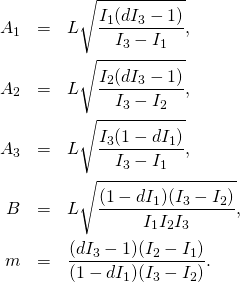
That is another purely mechanical task. Therefore again I give the result and show the REDUCE code verifying it.
(11) ![]()
where
(12) ![]()
We have differential equation for ![]() . We need to solve it. Van Zon and Schofield as it seems got tired towards the end of their paper and they did give us a nice formula. We will get such a nice formula in the next post.
. We need to solve it. Van Zon and Schofield as it seems got tired towards the end of their paper and they did give us a nice formula. We will get such a nice formula in the next post.





Przepraszam, że po polsku, ale angielski u mnie tylko w jedną stronę działa.
Wrócę jeśli można do tego:
http://arkadiusz-jadczyk.eu/images/tbh1ab.gif
i do pojedynczego nieskończonego fikołka przy d = 0,5
Którą trajektorię wybierze – lewą czy prawą?
Dobre pytanie. W tym przypadku są cztery możliwośći. Przypadek ten omówię w jednej z najbliższych notek.
For d = 0.5 left and right trajectory are the same. You can’t tell which is which. You can’t tell if “the leg of the T attacks “air” by the grey side and by the red side alternately” because there is no second somersault in that case.
I think it is more complicated. I will address this issue in the post I am working on now.
@arkajad
“I think it is more complicated.”
I am anxious to know what you think is more complicated with that simple merge of two kinds of trajectories. I armed myself with patience.
Yes, patience, please. Today is Laura’s birthday. So we have events at home. We are just watching the Pink Floyd in the Pulse
So I am not sure if I will manage to do the post still today …
But remember: for d=0.2 we have four different non-trivial trajectories (and two trivial ones)
“… for d=0.2 we have four …”
In base four system of course.
Jeśli skompresujemy t(-∞, +∞), to różnica pojawić się musi, inaczej by nie było różnicy trajektorii powrotnej.
For d = 0.5 there is no return trajectory.
Tak, powrotnej nie ma, ale dochodzimy do punktu, który by był jej początkiem – gdyby ta powrotna była.
Zresztą sam nieskończony fikołek trochę umowny, matematyczny raczej, a nie fizyczny.
@Bjab. Thank you for corrections!!!
:)
Have been trying to follow the reasoning in the Reduce code. The only way I can solve for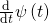 to get
to get 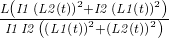 is effectively set
is effectively set 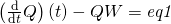
 works.
works.
eq1 has elements [1,3] and [2,3]=0. equating the equivalent element of
Equating to non zero elements of eq1 I can’t get to work properly. What am I doing wrong?
Have I missed something in the logic?
I would have to see exactly what you are doing.
The matrix has 3×3=9 entries. Five of the are automatically 0.
From the other four, two are proportional to sin, and two to cos.
Demanding the proportionality coefficients to be zero gives us what we need.
The same condition in each of the four cases.
So shouldn’t what Ronan has labeled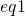 be set to zero?
be set to zero?
I would think so. That is why I would like to know more details.
You are corect. As soon as I read your reply I saw the error in my reasoning. What I do not understand is eq1 in the Reduce code. Why does it give the values for d(psi(t))/dt.
I went back and reread to blog entry but I am missing the logic in the principle of the matrix manupilation on that point.Iwill reread it again.
In (3):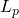 ->
->

equations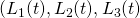 ->
->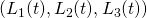
equations
->
(3 in subscript)
Thank you all fixed.