Dzhanibekov effect – Part 4: The equations of motion

Posted on by arkajad

The equations of motion

I have started the Dzhanibekov effect series with quaternions, but that is because of my personal attraction to quaternions. Some years ago I coauthored a paper on Quaternions and Monopoles. The monopoles there are the exotic “magnetic monopoles” that are lake fairies. Some physicist say they have seen them in the woods, but the majority of physicists take it as a joke. Quaternions are also somewhat exotic. I do not know if magnetic monopoles have any relation to Dzhanibekov effect, though, in fact they may have one – but that is for the physics of the future. For the physics of today, for the physics of a cosmic spinning and flipping nut, we need the physics of a rigid body. That is part of classical mechanics.

According to Wikipedia

In physics, a rigid body is an idealization of a solid body in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it.

I should say that the concept of a rigid body becomes somewhat iffy when we want to take into account what Albert Einstein taught us about first special, and then general relativity. I did not see yet a satisfactory relativistic theory of Dzhanibekov effect. What I know is that some physicists trying to sell their fantastic ideas to the investors (example G. Shipov) try to relate Dzhanibekov effect to “torsion fields” and “4D gyroscopes“. I have published some comments on this subject in International Journal of Unconventional Science. “Comments on Chapter 5 of G. I. Shipov’s “A Theory of Physical Vacuum”. Part I” is available in English. The second part, dealing with Shipov’s “4D gyroscopes” is for now available only in Russian, but it will be translated into English soon. A. Jadczyk on G. Shipov's 4D gyroscopes

But that is all in the exotic sphere. Interesting, for sure, but my aim is to describe the physics and mathematics of Dzhanibekov effect using old and good classical mechanics of Newton and Euler.

So, let us go now to the business. I am switching to math now. But remember, this is a blog., and it is interactive. If you do not ask questions – I will be assuming that you understand what I am writing. But if you want me to explain what is, for instance, “inertial reference system” or “center of mass” or “principal axes” – just ask, and I will explain in as many words and in as many posts as necessary.

We consider a free rigid body, observed form an inertial reference system, rotating with a fixed point at the center of its mass. Let \mathbf{E}_1(t), \mathbf{E}_2(t), \mathbf{E}_3(t) be an orthonormal frame corotating with the body, and aligned with its principal axes, and let \mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3 be an inertial laboratory frame, both centered at the center of mass of the body. The two frames are related by time-dependent orthogonal matrix A(t)

\mathbf{E}_i=A_{ij}\mathbf{e}_j,\quad X_i= A_{ij}x_j,

Then

Q= A^{-1}=A^t,

is often called the attitude matrix. For a rotating body, if X_i are coordinates of a fixed point in the body, then its coordinates in the laboratory system change in time:
{\bf x}(t)=Q(t){\bf X}.

Differentiating we get

\frac{d{\bf x}(t)}{dt}=\frac{dQ(t)}{dt}{\bf X}=\frac{dQ}{dt}Q^{-1}(t)\,{\bf x}(t).

The matrix Q(t) is orthogonal, Q(t)Q(t)^t=I, therefore, by differentiating, the matric \frac{dQ(t)}{dt}Q(t)^{-1} is antisymmetric. Every antisymmetric 3\times 3 matrix W can be written as

W = W({\bf v})=\begin{pmatrix}0& -v_3&v_2\\v_3&0&-v_1\\-v_2&v_1&0.\end{pmatrix}

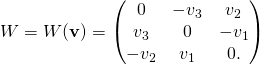
Writing \frac{dQ(t)}{dt}Q(t)^{-1}$ as $W(\boldsymbol{\omega}(t)):

(*)   \[ \frac{dQ(t)}{dt}Q(t)^{-1}=W(\boldsymbol{\omega}(t)),\]

we find that

\frac{d{\bf x}(t)}{dt}=\frac{dQ(t)}{dt}Q(t)^{-1}{\bf x}(t)=\boldsymbol{\omega}(t)\times{\bf x}(t).

The vector \boldsymbol{\omega}(t) is the angular velocity vector in the laboratory frame.

We denote by \boldsymbol{\Omega} the body representative of the angular velocity vector \boldsymbol{\omega}, where we skip the time dependence, with components \Omega_1,\Omega_2,\Omega_3.
Thus

\boldsymbol{\omega}= Q \boldsymbol{\Omega},

W(\boldsymbol{\omega})=QW(\boldsymbol{\Omega})Q^t,

and, from Eq. (*)

W(\boldsymbol{\Omega})=Q^T\dot{Q},

where \dot{Q}=dQ(t)/dt. In the body frame the inertia tensor I is diagonal I=\mathrm{diag}(I_1,I_2,I_3). The angular momentum vector \mathbf{L} in the body frame is then given by the formula

\mathbf{L}=I\boldsymbol{\Omega},

and the Euler equations for the free rotation read:

\dot{\mathbf{L}}=\mathbf{L}\times I^{-1}\mathbf{L}.

When written componentwise in terms of the angular velocity components they take the well known form

(1)   \begin{eqnarray*} \frac{dL_1}{dt}+(\frac{1}{I_2}-\frac{1}{I_3})L_2L_3&=&0,\nonumber\\ \frac{dL_2}{dt}+(\frac{1}{I_3}-\frac{1}{I_1})L_3L_1&=&0,\nonumber\\ \frac{dL_3}{dt}+(\frac{1}{I_1}-\frac{1}{I_2})L_1L_2&=&0.\nonumber \end{eqnarray*}

(2)   \begin{eqnarray*} A_1&=&\sqrt{\frac{I_1(dI_3-1)}{I_3-I_1}},\nonumber\\ A_2&=&\sqrt{\frac{I_2(dI_3-1)}{I_3-I_2}},\nonumber\\ A_3&=&\sqrt{\frac{I_3(1-dI_1)}{I_3-I_1}},\nonumber\\ B&=& \sqrt{\frac{(1-dI_1)(I_3-I_2)}{I_1I_2I_3}},\nonumber\\ m&=&\frac{(dI_3-1)(I_2-I_1)}{(1-dI_1)(I_3-I_2)}.\nonumber \end{eqnarray*}

Now we need to solve explicitly Euler’s equations, which is just the first part of the task. Then we have to find the attitude matrix. Then we have to use these explicit solutions in order to produce realistic animations of Dzhanibekov’s effect. It is a lot of work, especially if one is going to reveal all the details. So, let us see where it will lead us to.

4 thoughts on “Dzhanibekov effect – Part 4: The equations of motion”

  2. Test of Registeration. My question was Qusetion:- what is the difference between “inertial reference system” and “inertial laboratory frame”? I guess one tumbles with the object.
    I now understand after re-reading. The “inertial reference system” is rotating with the object and the “inertial laboratory frame” is fixed.

  3. I am using here “inertial reference frame” and “inertial laboratory frame” to mean the same – a frame attached to a body that is not rotating nad not accelerating with respect to the fixed stars, or, if you wish, to “Aether”. Well, approximately.

    From Wikipedia:

    …
    Newton viewed the first law as valid in any reference frame that is in uniform motion relative to the fixed stars;[32] that is, neither rotating nor accelerating relative to the stars.[33] Today the notion of “absolute space” is abandoned, and an inertial frame in the field of classical mechanics is defined as:[34][35]

    An inertial frame of reference is one in which the motion of a particle not subject to forces is in a straight line at constant speed.
    ….

    On the other hand there is another frame, tumbling with the object. That frame is not an inertial frame (there is a centrifugal force acting within this frame). I will often call it the rotating frame. I am assuming that this frame is oriented so that its axes point in the directions of “principal axes” see Moment of inertia in Wikipedia

    If you would like to have further clarification – do not hesitate to ask.

  4. Thank you for the above. Oddly I had been meaning to study up on Inertia matrices for a good while now. My nest question is on the form of inputs to Q or A. I am treating it as a rotoation matrix made up from RotZ . RotY .RotX where the individual matrices are of the form RotZ=[[cos(omega1 t),-sin(omega1 t),0],[sin(omega1 t),cos(omega1 t),0],[0,0,1]] ,omega2 for Y and omega3 for X. Difficult to copy and paste anything nice looking. Following the process it produced the antisymmetric matrix fine. Have produced the 3 Euler eqns. Can you explain where A1 to m come from.
    I find it takes a lot of thinking about to understand each step

Leave a Reply