I did not post anything new on my blog yesterday. Not because it is Saturday. And not because I was celebrating the fact that I have just received a personal email from Владимир Джанибеков – Vladimir Dzhanibekov, the former Cosmonaut and Commander of the French Legion of Honour – while I writing the series about Dzhanibekov effect.
 I did not write my regular post yesterday because all the day long I was busy solving a mystery. It was a real detective work. It needed joined powers of Sherlock Holmes and Hercule Poirot while working on the case of inverted modulus. What is the the case of inverted modulus I will soon explain. Roughly it is a very clever crime, with very well hidden motives and very famous participants. And yes, it is directly related to Dzhanibekov effect! By the way in his email to me of yesterday Dzhanibekov confesses that his effect is still a mystery for him. So we have a double mystery, a mystery within a mystery. Indeed doubled efforts are needed. According to one opinion:
I did not write my regular post yesterday because all the day long I was busy solving a mystery. It was a real detective work. It needed joined powers of Sherlock Holmes and Hercule Poirot while working on the case of inverted modulus. What is the the case of inverted modulus I will soon explain. Roughly it is a very clever crime, with very well hidden motives and very famous participants. And yes, it is directly related to Dzhanibekov effect! By the way in his email to me of yesterday Dzhanibekov confesses that his effect is still a mystery for him. So we have a double mystery, a mystery within a mystery. Indeed doubled efforts are needed. According to one opinion:
“While both of them are arrogant and conceited, I believe Poirot is cooler and smarter!(There I said it…) He is not doing things in a grandiose manner as Holmes is prone to do, but mostly working out things in that egg-shaped head of his. He is also very polite though a wee bit condescending towards his interviewees, but is always a thorough gentleman and seems to empathize about the vicissitudes of a criminal mind. Holmes on the other hand comes across as being cold most of the times, though I am not sure there might have been times when he was a little more humanisque than a precise surgeon who does his job.”
But, well, we are not discussing here the literary characters of Arthur Conan Doyle and Agata Christie – we are dealing with reality, not a fiction, have a real case, even if it is in the Platonic world of mathematical concepts. So what is the case about?
In Jacobi elliptic functions – Definition as trigonometry following ideas from William A. Schwalm I introduced Jacobi elliptic function ![]() defined for all real
defined for all real ![]() and
and ![]() At the same time I knew that it would be cute to have it defined also for
At the same time I knew that it would be cute to have it defined also for ![]() I checked several textbooks, and have found that many authors explicitly assume that
I checked several textbooks, and have found that many authors explicitly assume that ![]() while others are suspiciously silent about the allowed values of
while others are suspiciously silent about the allowed values of ![]() The “definition as trigonometry” that I have presented following the Wikipedia does not make sense at all for
The “definition as trigonometry” that I have presented following the Wikipedia does not make sense at all for ![]() But what about the formal definition as used for instance in Abramowitz-Stegun Handbook:
But what about the formal definition as used for instance in Abramowitz-Stegun Handbook:

The same handbook gives also the following conversion formulas:

Therefore it is apparently possible to have ![]() If so, the why so many textbooks assume explicitly
If so, the why so many textbooks assume explicitly ![]() ? Allowing for
? Allowing for ![]() would allow us to write down the explicit solution of Euler equations for free asymmetric top in one formula, independent of the value of the kinetic energy. Yet in so many books and papers the authors are using two different formulas for two different kinetic energy ranges. Why?
would allow us to write down the explicit solution of Euler equations for free asymmetric top in one formula, independent of the value of the kinetic energy. Yet in so many books and papers the authors are using two different formulas for two different kinetic energy ranges. Why?
I asked myself this question because I am trying to understand the subject I am writing about. And so yesterday I was all day long busy with solving the mystery. Finally I have solved it – to my satisfaction. And now I will describe my solution in detail. This morning, after I already started writing this post, I have found essentially the same solution an a paper Elliptische Integrale und Funktionen nach Jacobi by Ralph Hopke, and in Chapter 3.9 Further Transformations of the Modulus of the monograph Elliptic Functions and Applications by Derek F. Lawden. And yet I am going to explain here the solution in as simple terms as I can I hope that someone will find it useful.
The original name of Jacobi elliptic sn function was sinus amplitudinis. One contemplates the integral
(1) ![]()
and calls ![]() the amplitude
the amplitude ![]() of
of ![]() where
where ![]() Then
Then ![]() is defined as
is defined as ![]() that is as
that is as ![]() – that is how sinus amplitudinis was invented.
– that is how sinus amplitudinis was invented.
First let us contemplate the integral 1. If ![]() the integral is well defined (produces a finite number) for all finite values of
the integral is well defined (produces a finite number) for all finite values of ![]() The integrand is always positive, therefore
The integrand is always positive, therefore ![]() is strictly increasing function of
is strictly increasing function of ![]() The inverse function exists,
The inverse function exists, ![]() is well defined.
is well defined.
But what if ![]() ? From the definition we see that
? From the definition we see that ![]() is antisymmetric function of
is antisymmetric function of ![]() therefore let us restrict ourselves to
therefore let us restrict ourselves to ![]() nonnegative. If
nonnegative. If ![]() is smaller that the critical value
is smaller that the critical value ![]() defined by
defined by ![]() , the integral is finite and is an increasing function of
, the integral is finite and is an increasing function of ![]()
For ![]() approaching
approaching ![]() the integral becomes infinite. Therefore the inverse function
the integral becomes infinite. Therefore the inverse function ![]() is well defined for all
is well defined for all ![]() also for
also for ![]()
It is only that the range of ![]() becomes finite for
becomes finite for ![]() but there is nothing wrong with it. We will deal with the beauty of Jacobi’s amplitude in the next post. Here we are interested in sinus amplitudinis. WE now know that it is well defined for all real values of the modulus
but there is nothing wrong with it. We will deal with the beauty of Jacobi’s amplitude in the next post. Here we are interested in sinus amplitudinis. WE now know that it is well defined for all real values of the modulus ![]() Therefore it should be now possible, using the definition, to prove the mysterious modulus transformation formula from Abramowitz-Stegun, which can be written as:
Therefore it should be now possible, using the definition, to prove the mysterious modulus transformation formula from Abramowitz-Stegun, which can be written as:
(2) ![]()
The proof of the above formula is, as Sherlock Holmes would say, elementary. Perhaps, but not without Watson’s hard work and not without the hindsight from Poirot after his conversation with Hastings. It is a simple case of a clever change of variables in the integral.
(3) ![]()
According the definition we write
(4) 
and set
![]()
Now, instead of ![]() we introduce
we introduce ![]() so that
so that
(5) ![]()
This is always possible since ![]() therefore
therefore ![]() so that there exists
so that there exists ![]() satisfying Eq. 5. We then have
satisfying Eq. 5. We then have
![]()
From Eq. (5) we also have
![]()
or
(6) ![]()
Thus
![Rendered by QuickLaTeX.com \[\int_0^\phi\frac{d\theta}{\sqrt{1-\frac{1}{k^2}\sin^2\theta}}= \int_0^{\tau(\phi)}\frac{k\cos\tau}{\cos\tau\,\cos\theta}d\tau =k\int_0^{\tau(\phi)}\frac{d\tau }{\cos\theta}.\]](http://arkadiusz-jadczyk.eu/blog/wp-content/ql-cache/quicklatex.com-877d6e15984f0385dc34da4429613a90_l3.png)
But from Eq. (5) we have that ![]() therefore
therefore
(7) 
Comparing with Eq. (4) we get
(8) 
Let us consider now the left hand side of Eq. (2):
![]()
Using the definition of ![]()
![]()
where ![]() is such that
is such that
![]()
We thus see that ![]() and, using Eq. (5):
and, using Eq. (5):
![]()
So, essentially, the mystery is solved and the case can be closed.
I must confess that at the beginning, instead of substitution as in Eq. (5) I was trying ![]() It did not work though.
It did not work though.
The next post will be about the beauty of Jacobi’s amplitudinis.



@BJAB Thank you for the errata – that was a lot!!!!
“,,, the range of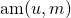 becomes finite for m>1,”
becomes finite for m>1,”
What about m=1 ?
For m=1 the integral diverges for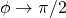
The graph of am(u,1) below
It approaches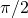 for
for 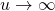
I will fix the sentence in my post. Have to think about it.
I recognize this shape.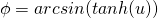
It is
:)