Jacobi Elliptic sn – the case of a stuttered sinus

Posted on 2017/01/12 by arkajad

In my last post I introduced Jacobi elliptic sinus, the function sn(u,m), with u real, and 0\leq m\leq 1. One has to be careful with notation here. Let us have a look at the definition as it is given on Wolfram’s pages:

It is almost the same, but not the same as one from “Handbook of Mathematical Functions“, Ed. Milton Abramowitz and Irene A. Stegun:

Here Abramowitz and Stegun write simply sn u, but later on they use the notation sn(u|m), where m=k^2 of Wolfram. Wolfram’s Mathematica is using JacobiSN(u,m). Maple is using JacobiSN(u,k).
Matlab warns the user:

We will use sn(u,m).
The parameter k=\sqrt{m} is sometimes called the “modulus”. The shape of the function depends on the value of m. When m=0 we have just ordinary sinus:

At the other extreme, for m=1, sn is nothing else but the hyperbolic tangent:

In between, for 0<m<1, it is what I would dare to call a “stuttering sinus“. This stuttering is not seen at all for m=0.1 It looks just as if the period became a little longer:

and it is hard to notice for m=0.9

But for m=0.9999999 we get

It almost looks like the hyperbolic tangent, but when we zoom out we can see the stuttering:

Clear case of stuttering

The graphs looks somewhat like that of a rectangular signal. There are “flips” and then there are longer and longer periods when the function is almost constant – between the flips. This is the main characteristic of Dzhanibekov effect: there are almost pure rotation periods, and sudden flips when the axis suddenly reverses the direction. But for all values of m the function is periodic (for m=1 we have an exception – we have infinite period).

For m=0 the period is 2\pi, then slowly grows, but for m very close to 1 it becomes very sensitive to the value of m. For this reason every repetition of the Dzhanibekov effect as seen in the movies taken in space would probably give a different period.

Print 🖨 PDF 📄 eBook 📱
This entry was posted in Elliptic functions. Bookmark the permalink.

17 Responses to Jacobi Elliptic sn – the case of a stuttered sinus

  1. arkajad says:
    2017/01/12 at 15:16

    To use latex in comments you should write, at the beginning of your comment [\rm{latexpage}]. Then we can see latex at work

        \[ r=\frac{1}{\sqrt{1-m\sin^2\theta}}\]

    Syntax explained here.

  2. Bjab says:
    2017/01/12 at 19:12

    “In between, for 0<m<1, it is what I would dare to call a “stuttering sinus“"
    Poetry piece.

    • arkajad says:
      2017/01/12 at 20:30

      Yes. In fact: not a very ambitious. But: blogs are good places for publishing poetry pieces. On my blog I will sometimes make jokes, sometimes write something surrealistic. Blogs are personal. I am not pretending to know a lot. I often make mistakes. Blogs are for sharing ideas. Wikipedia has different goals and therefore different duties.

  3. Bjab says:
    2017/01/12 at 19:17

    “for m=1, sn is nothing else but the hyperbolic sinus”

    “It almost looks like the hyperbolic sinus”

    I was used to the different appearance of the graph of hyperbolic sinus.

  4. arkajad says:
    2017/01/13 at 15:54

    @BJAB

    ““for m=1, sn is nothing else but the hyperbolic tangent”
    Would you prove it?”

    OK I did it. And it was a good exercise. Thank you for this question.
    For m=1 we have

        \[u=\int_0^\phi 1/\sqrt{1-\sin^2\theta}d\theta =\int_0^\phi \frac{1}{\cos \theta}\, d\theta \]

    Then, from the definition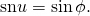 \mathrm{sn} u = \sin\phi . So I asked Mathematica to find the integral.
    I got

        \[u= -\log(\cos(\phi/2)-\sin(\phi/2))+\log(\cos(\phi/2)+\sin(\phi/2))\]

    It looks good. It can be verified by differentiation, and for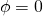 \phi=0 we get 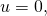u=0, as it should be.(Wikipedia gives the answer in a somewhat different form) It looks complicated, but I knew what the answer should be anyway. The answer simplified to

        \[u = \log\left(1+\frac{2}{\cot(\phi/2)-1}\right)\]

    Then I asked to calculate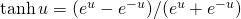 \tanh u = (e^u-e^{-u})/(e^u+e^{-u}) using the trigonometric identity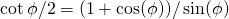 \cot\phi/2=(1+\cos(\phi))/\sin(\phi)
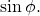
    The answer was, surprise-surprise …\sin\phi.

  5. Bjab says:
    2017/01/13 at 21:35

    Ark,
    during loging I get prompt:
    “2 attempts remaining.”

    It is rather frustrating.

    Can you do something with it?

  6. Bjab says:
    2017/01/13 at 21:47

    Ark,
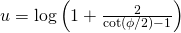
    thank you for the proof.
    I’ve checked it. I’ve found one misspelling. I think that there should be 2 in numerator
    u = \log\left(1+\frac{2}{\cot(\phi/2)-1}\right)

Leave a Reply