Yesterday was a day with no apparent progress. Some days are diamonds (living spiraling force) some days are stones (elliptic) – I wrote. And indeed, it was elliptic stone. But “apparently no progress” is not the same as “no progress whatsoever”. Yesterday was one of these days that Thomas Edison would classify as finding yet another way that will not work

“I have not failed 10,000 times. I have not failed once. I have succeeded in proving that those 10,000 ways will not work. When I have eliminated the ways that will not work, I will find the way that will work.”
Attributed to Thomas Edison
And today, for change, is a diamond. Well, perhaps not a real diamond, but zirconia at least.

After this introduction I go to math right away. Let me recall what my problem was: I was unable to solve one of the exercises in the notes by John Baez . As we learn from Wikipedia
is an American mathematical physicist and a professor of mathematics at the University of California, Riverside (UCR) in Riverside, California.
….
His physicist uncle, Albert Baez (inventor of the X-ray microscope and father of singer and progressive activist Joan Baez), interested him in physics as a child
I do not know that exactly is “progressive activist”, but that is not the problem. The problem was that John Baez gave some hints how to prove that Jacobi elliptic sn function is periodic not only with real, but also with imaginary period. The suggested trick involved using gravity that attracts to the sky instead of attracting to the Earth, as we know it. But I could not find how to use the trick even after finding the exercise solved in the textbook on elliptic functions by Armitage and Eberlein – my previous post Some days are diamonds (living spiraling force) some days are stones (elliptic) for details. And indeed my problem was with the details. While I had a general idea about what to do, when it came to justifying rigorously every step – here I have found an insurmountable hole.
This morning however I woke up with an idea. And lo and behold – it worked. So we have a progress. Let me explain.
Suppose we want to prove that the function ![]() defined, say, by power series
defined, say, by power series ![]() is periodic. How to do it? One possible way is by first proving the formula known from the school:
is periodic. How to do it? One possible way is by first proving the formula known from the school:
![]()
Suppose we know that the above addition formula is true. Suppose additionally we know that ![]() and
and ![]() The setting
The setting ![]() in the addition formula we get
in the addition formula we get
![]()
and thus
![]()
So, we have the period. But first we need the addition formula. Why not to apply the same method to ![]() ? We need addition formula. This can be found online, Eq. (48) in Jacobi Elliptic Functions. It reads:
? We need addition formula. This can be found online, Eq. (48) in Jacobi Elliptic Functions. It reads:
(1) ![]()
But how to prove it?
First I thought: I will simply follow Euler’s method that takes just a page in a little old book that I have: F. Bowman, “Introduction to Elliptic Functions with Applications”. BUt after a while I realized that this method, invented by Euler, needs a certain amount of intelligence, it is using some tricks. There must be a simpler method, a “no-brain method”. Once we know what we want to prove, we can ask the computer to do it for us! Then it will take no space and no time at all. You press “Enter”, and the all the work is done. And this is how I did it.
Below are the details, so that, if you would like to learn how to do such things, follow me!
Let us denote the right hand side of Eq. (??), thought of as a function of ![]() with
with ![]() and
and ![]() fixed, by
fixed, by ![]() We want to prove that
We want to prove that ![]() But how is the function
But how is the function ![]() defined? In Derivatives of Jacobi elliptic am, sn, cn, dn, we have derived the formula
defined? In Derivatives of Jacobi elliptic am, sn, cn, dn, we have derived the formula
![]()
Taking square of both sides and using
![]()
we have
(2) ![]()
This last differential equation, together with the initial value ![]() determines the function
determines the function ![]() uniquely (up to a sign, but sign is not a problem for us).
uniquely (up to a sign, but sign is not a problem for us).
So, we need to prove that our function ![]() satisfies the differential equation:
satisfies the differential equation:
(3) ![]()
That ![]() is obvious form the definition and the fact that
is obvious form the definition and the fact that ![]() Since we do have the formulas for derivatives of elliptic functions, we can let the computer to verify Eq. (??). And it is easy. You need REDDUCE program. It is a free computer algebra program and it can run almost on any platform. And it is only 50 MB!
Since we do have the formulas for derivatives of elliptic functions, we can let the computer to verify Eq. (??). And it is easy. You need REDDUCE program. It is a free computer algebra program and it can run almost on any platform. And it is only 50 MB!
Then we need to tell reduce what to do. Here is my code:
OPERATOR cn,sn,dn,h;
h(v):=(snu*cn(v)*dn(v)+sn(v)*cnu*dnu)/(1-m*snu^2*sn(v)^2);
dh:=(DF(h(v),v));
For all v let DF(sn(v),v)=cn(v)*dn(v);
For all v let DF(cn(v),v)=-sn(v)*dn(v);
For all v let DF(dn(v),v)=-m*sn(v)*cn(v);
dh:=dh;
w:=dh^2-(1-m*h(v)^2)*(1-h(v)^2);
w;
for all v let dn(v)^2=(1-m*sn(v)^2);
w;
for all v let cn(v)^2=1-sn(v)^2;
let dnu^2=1-m*snu^2;
let cnu^2=1-snu^2;
w;
wn:=NUM(w);
wn:=wn;
OFF NAT;
OUT “H:\Reduce MyFiles\resadd.txt”;
wn;
SHUT “H:\Reduce MyFiles\resadd.txt”;
END;
You can replace “C:\resadd.txt” with whatever you want as the output file. You save the code above as a text file somewhere on your hard drive. The I have saved it as “add1.red” on my drive H in a subdirectory. Then you start REDUCE. It opens a window. Here is what I have typed in this window:
You change the path, so that it is to your file. You type what you see above, and press ENTER. It takes less than a second and the output is written. You can look at it and it should tell you the same as my says, namely “0”.
And that is the end of the proof. QED. Quod erat demonstrandum. The diamond day.
A cigar, but no mirrors.
But we can now return to the imaginary time period of the pendulum.

And so it is. We know today that Galileo was wrong. His assertion was false. Which did not prevent him from becoming famous. He has discovered “an approximate truth”, that is, strictly speaking, “a lie”. Life is complicated.
As it is said:
According to Homer, the philosophy of the ancient world was that there was a third element that linked the opposing elements. Between the body and the soul, there is the spirit. Between life and death there is the transformation that is possible to the individual, between father and mother there is the child who takes the characteristics of both father and mother, and between good and evil there is the SPECIFIC SITUATION that determines which is which and what ought to be done.




@Bjab
Thanks for the erratum – twice!.
In (3) we have
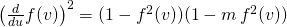
but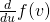 is equal to zero (due to u is not v), isn’t it?
is equal to zero (due to u is not v), isn’t it?
It was my mistake. Should be d/dv. Fixed. Thank you!
“But we can now return to the imaginary time period of the pendulum.”
What about the real time period?
Our client – our master. It will appear today.