This is not an independent post or note or whatever. It is a continuation. In fact it is the continuation of Approaching the ultimate answer for m<1. We have approached enough. We are ready.
There was a moment’s expectant pause while panels slowly came to life on the front of the console. Lights flashed on and off experimentally and settled down into a businesslike pattern. A soft low hum came from the communication channel.
“Good morning,” said Deep Thought at last.
“Er … good morning, O Deep Thought,” said Loonquawl nervously, “do you have … er, that is …”
“An answer for you?” interrupted Deep Thought majestically. “Yes. I have.”
The two men shivered with expectancy. Their waiting had not been in vain.
“There really is one?” breathed Phouchg.
“There really is one,” confirmed Deep Thought.Douglas Adams, The Hitchhiker’s Guide to the Galaxy
We did not get to the answer yesterday, but today is the day. We will be using the formulas from the last post. Here they are again, repeated for your convenience:
(1) 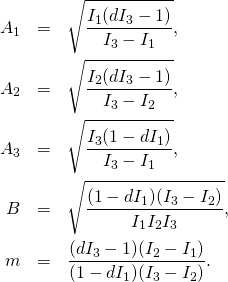
The solution ![]() of the Euler’s equations has two trajectories: one with
of the Euler’s equations has two trajectories: one with ![]() is given by
is given by
(2) 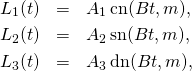
while the other one, with ![]() is given by
is given by
(3) 
With constants ![]() and
and ![]() defined as
defined as
(4) 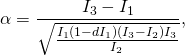
(5) ![]()
we set the phase variable ![]() as
as
(6) ![]()
where the Jacobi function ![]() is defined as
is defined as ![]()
Then the quaternionic attitude solution is given by ![]() with
with
(7) 
We consider Example Four with
(8) 
(9) 
![]() is negative, the therefore we take option as in Eq. 3). We calculate
is negative, the therefore we take option as in Eq. 3). We calculate ![]() that reproduces the initial angular momenta. The method is known from the previous posts:
that reproduces the initial angular momenta. The method is known from the previous posts:
(10) ![]()
(11) ![]()
So we have ![]() At
At ![]() our angular momentum is the same as angular momentum in example 4 at
our angular momentum is the same as angular momentum in example 4 at ![]() We calculate
We calculate ![]() from Eq'(7)
from Eq'(7)
![]()
(12) 
thus
(13) ![]()
We verify that we have indeed a unit quaternion:
![]()
Thus the inverse quaternion is the same as conjugated one:
![]()
In the Example 4 the initial quaternion, at ![]() is
is ![]() . Therefore in order for our solution to reproduce the initial data of the example we set
. Therefore in order for our solution to reproduce the initial data of the example we set
(14) ![]()
The final time in Example 4 is ![]() Therefore we calculate
Therefore we calculate
(15) ![]()
where the multiplication is the quaternion multiplication.
Calculated with Mathematica the answer is
(16) 
The result from the Fortran code in the file out_example4.dat is
-0.3676198430772359
-0.6306293413288832
-0.6127232632258010
0.3028737154869889

It seems that therefore that we have obtained the ultimate answer. At least for quaternions. We need to get it also for rotation matrices. So the saga will continue.