When I was in the middle of writing this post, question came in a comment from Bjab
New Note after posting everything here: As has just been pointed to me by Ronan, I have already covered this issue in Infeld, Einstein and blogging . While, there is no harm in covering the same issue twice, the fact that I have forgotten tells something about the workings of my memory. But collective memory (of all readers) seems to be the answer.
Ark,
where can I find, in your posts, formulas for A1, A2, A3, B, m for m>1 ?(For m<1 and m=1 they are in posts:"Taming the T-handle" and "Taming the T-handle – continued"
I checked, and indeed I could not find the place where I have treated this problem with clarity. It is my ambition to write extremely clear, better in this respect than anyone else in the whole universe, but here we have a hole. Since this post was anyway supposed to be exactly about the case of ![]() I will start with describing the case in details (and, as we know, the devil is hiding just there).
I will start with describing the case in details (and, as we know, the devil is hiding just there).

To begin with the beginning: when considering a free rigid body rotating about its center of mass, the most important parameter characterizing the rotation is the parameter ![]() defined as the ratio of the doubled kinetic energy (that is constant during the motion) to the square
defined as the ratio of the doubled kinetic energy (that is constant during the motion) to the square ![]() of the angular momentum vector (that is also constant during the motion). In order to simplify the notation let us assume that
of the angular momentum vector (that is also constant during the motion). In order to simplify the notation let us assume that ![]() is normalized so that
is normalized so that ![]() Then
Then
(1) ![]()
where ![]() are the principal moments of inertia, and
are the principal moments of inertia, and ![]() are the components of the angular momentum vector with respect to the frame attached to the body. It follows almost directly from the definitions that the value of
are the components of the angular momentum vector with respect to the frame attached to the body. It follows almost directly from the definitions that the value of ![]() is in the interval
is in the interval ![]() The case of
The case of ![]() is very special, there is only one flip of the body – it is “the archetype of Dzhanibekov effect”.
is very special, there is only one flip of the body – it is “the archetype of Dzhanibekov effect”.
The first step in finding explicit solution to the equations of motion is to solve Euler’s equations:
(2) 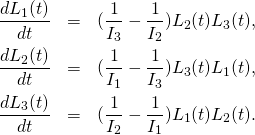
A solution is given by the following explicit formula adapted from Solving Euler’s equations:
In Solving Euler’s equations the solution is given for ![]() . To get the solution for
. To get the solution for ![]() we simply multiply the constants
we simply multiply the constants ![]() from there by
from there by ![]() to obtain
to obtain
(4) 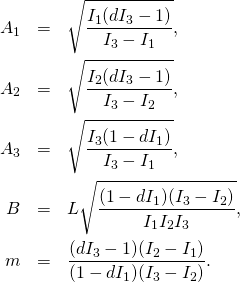
In the formulas (3) Jacobi elliptic functions ![]() are somewhat formally extended to cover the case of
are somewhat formally extended to cover the case of ![]() that corresponds to
that corresponds to ![]() It is safer to transform these formulas using the conversion formulas (see More is different and links from there)
It is safer to transform these formulas using the conversion formulas (see More is different and links from there)
Let us call ![]() Then, with
Then, with ![]()
![]() become
become
(8) 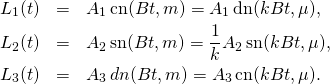
We see that perhaps it is useful to introduce new constant ![]() that is equal to the old
that is equal to the old ![]() divided by
divided by ![]() . We have
. We have
![Rendered by QuickLaTeX.com \[1/k=\sqrt{1/m}=\sqrt{\frac{(1-dI_1)(I_3-I_2)}{(dI_3-1)(I_2-I_1)}}.\]](http://arkadiusz-jadczyk.eu/blog/wp-content/ql-cache/quicklatex.com-8ea72417649f48e7db9fec73aeabf324_l3.png)
Therefore, after some little calculation, we get
![Rendered by QuickLaTeX.com \[ A_2/k=\sqrt{\frac{I_2(dI_3-1)}{I_3-I_2}}\sqrt{\frac{(1-dI_1)(I_3-I_2)}{(dI_3-1)(I_2-I_1)}}=\sqrt{\frac{I_2(1-dI_1)}{I_2-I_1}}.\]](http://arkadiusz-jadczyk.eu/blog/wp-content/ql-cache/quicklatex.com-d7d8f062fccef254169f8b636c789a65_l3.png)
This will be our new ![]() It is also useful to introduce new
It is also useful to introduce new ![]() that equals to
that equals to ![]() times old
times old ![]() . We have
. We have
![Rendered by QuickLaTeX.com \[kB=\sqrt{\frac{(dI_3-1)(I_2-I_1)}{(1-dI_1)(I_3-I_2)}}\sqrt{\frac{(1-dI_1)(I_3-I_2)}{I_1I_2I_3}}=\sqrt{\frac{(dI_3-1)(I_2-I_1)}{I_1I_2I_3}}\]](http://arkadiusz-jadczyk.eu/blog/wp-content/ql-cache/quicklatex.com-b13a6c72085d07179c0b66224fa26157_l3.png)
This will be our new ![]() . Finally, we can now rename old
. Finally, we can now rename old ![]() into
into ![]() Altogether we obtain
Altogether we obtain
(9) 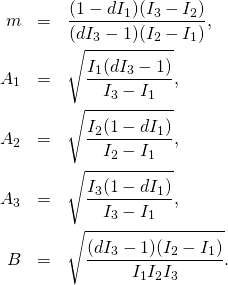
A solution of the Euler’s euqations for this case can be written as
(10) 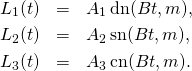
I wrote “a solution”. In fact it is almost the most general solution. Every solution can be obtained by shifting the time ![]() and, if necessary, putting minus signs in front of two of the three formulas for
and, if necessary, putting minus signs in front of two of the three formulas for ![]()
That was an extra for this post because of the question from Bjab. Now comes what I was going to post today originally.
This is a continuation from the previous post Spinning Gulliver among giants. Another example from the paper: Elena Celledoni, Antonella Zanna, et al. “Algorithm 903: FRB–Fortran routines for the exact computation of free rigid body motions.” ACM Transactions on Mathematical Software, Volume 37 Issue 2, April 2010, Article No. 23, doi:10.1145/1731022.1731033

I will make it short and sweet, because the reasoning will be like in Spinning Gulliver among giants. At the same time I will stress the differences. This should also help to understand the algorithm I am using for the case ![]() I am using Mathematica, and in the forthcoming posts I will mention how to adapt it to Maple (which at the same time will answer the comment from Ronan).
I am using Mathematica, and in the forthcoming posts I will mention how to adapt it to Maple (which at the same time will answer the comment from Ronan).
I am taking now “example0” from Fortran code examples that accompany the paper by Celledoni and Zanna. These examples can be downloaded in a zip file using the link to the code here. (though I got the file directly from one of the Authors – A.Z.).
The description of example0 in a Readme file: “driver_example0.f (example of FRB integration in a single step from 0 to Tfin). To be linked with frb_step.f”.
The initial data for this example are (I am decoding here their meaning)
Time to run:
1.0000000000000000e-01
Moments of inertia:
1.0000000000000000e+00
1.6487857827119290e+00
1.9720127096641928e+00
Initial angular momentum
-0.709894965287627e+00
-0.685144717153487e+00
0.163174308075589e+00
Initial attitude matrix (columnwise|)
-0.139359936806125e+00
-0.414251479478192e+00
-0.899430108326112e+00
-0.726901415681411e+00
-0.574008408466476e+00
0.376999574124619e+00
-0.672453076350874e+00
0.706335655874678e+00
-0.221126211350745e+00
At first I was playing with these data. But then, reading Readme.txt, I noticed that: “driver_example2.f (Like driver_example0.f, but uses quaternions in place for rotations). To be linked with quat_step.f“. So I checked example2, and I noticed that there the initial attitude matrix is given by the unit quaternion 1. That is the initial attitude matrix is the identity matrix as it was in the example we have already discussed in Spinning Gulliver. Therefore I decided to change the example and to use the identity matrix here as well. So I will be discussing the slightly modified version of the original example.
To Mathematica I enter these data:
Tfin = 0.1;
I1 = 1;
I2 = 1.6487857827119290;
I3 = 1.9720127096641928;
L10 = -0.709894965287627;
L20 = -0.685144717153487;
L30 = 0.163174308075589;
I checked that the initial angular momentum vector has indeed length 1, as it is supposed to have. We now calculate ![]()
Since ![]() we have the case when
we have the case when ![]()
This is more difficult case. The modulus ![]() (and
(and ![]() ) would come greater than 1. While Mathematica has elliptic functions with
) would come greater than 1. While Mathematica has elliptic functions with ![]() other software may have them only for
other software may have them only for ![]() We were discussing before how to convert from
We were discussing before how to convert from ![]() to
to ![]() . Here I will be using the results of our previous discussions. So,
. Here I will be using the results of our previous discussions. So, ![]() below will be already inverted, therefore smaller than 1. Here are the formulas for our case:
below will be already inverted, therefore smaller than 1. Here are the formulas for our case:
A1 = Sqrt[I1*(d*I3 – 1)/(I3 – I1)]
A2 = Sqrt[I2*(1 – d*I1)/(I2 – I1)]
A3 = Sqrt[I3*(1 – d*I1)/(I3 – I1)]
B = Sqrt[((d*I3 – 1)*(I2 – I1))/(I1*I2*I3)]
m = ((1 – d*I1)*(I3 – I2))/((d*I3 – 1)*(I2 – I1))
We get
A1 = 0.773709
A2 = 0.709067
A3 = 0.633541
B = 0.340743
m = 0.169391
In our simulations for this case in many previous posts we were using:
L1 = A1*JacobiDN[B*t,m]
L2 = A2*JacobiSN[B*t,m]
L3 = A3*JacobiCN[B*t,m]
But now we see that L10 is negative. This is a different Poinsot orbit. Therefore we have to change the sign of L1. We know that when we want to have Euler’s equations still satisfied, we have to change also one other sign. Let us choose L2 ( I could instead change L3, then ![]() would be different, but all the conclusions would be the same). Thus what we will use is
would be different, but all the conclusions would be the same). Thus what we will use is
L1[t_] = -Re[A1*JacobiDN[B*t, m]];
L2[t_] = -Re[A2*JacobiSN[B*t, m]];
L3[t_] = Re[A3*JacobiCN[B*t, m]];
We have put minus sign in the formula for L1[t] and L2[t].
The formula for ![]() is
is
![Rendered by QuickLaTeX.com \[\psi (\text{t$\_$})=\frac{(\text{I3}-\text{I1}) \Pi \left(-\frac{\text{I3} (1-d \text{I1})}{\text{I1} (d \text{I3}-1)};\left.\text{am}\left(\left.t \sqrt{\frac{(\text{I2}-\text{I1}) (d \text{I3}-1)}{\text{I1} \text{I2} \text{I3}}}\right|m\right)\right|m\right)}{\sqrt{\frac{\text{I1} \text{I3} (d \text{I3}-1) (\text{I2}-\text{I1})}{\text{I2}}}}+\frac{t}{\text{I3}};\]](http://arkadiusz-jadczyk.eu/blog/wp-content/ql-cache/quicklatex.com-c4da1991f62fc58bbd034ce8c13e0e4c_l3.png)
Note: I have not yet discussed the formula for ![]() for
for ![]() It needs to be discussed. But we will not be using it in this post anyway.
It needs to be discussed. But we will not be using it in this post anyway.
The rest goes like in the previous post. As before, we compute the amplitude
Thus, using Mathematica ArcTan function:
![]()
Notice that here I had to put minus sign in front of L20. That is because we have changed the sign in the formula for L2.
I use Mathematica and get
![]()
Then
![]()
The output file from the Fortan program gives both angular momentum and the attitude matrix at the final time. Let us first check angular momentum. Notice that even if I have changed the initial attitude matrix, this change does not affect the angular momentum. Therefore I can read the final angular momentum from the original output file. Here it is:
-0.708844791922432
-0.690514805418774
0.143973485273913
We go to Wolfram Alpha, enter there our data for ![]() :
:
0.773709 JacobiDN[0.340743*(3.98931+0.1,0.169391)
and obtain the result: 0.7088446163317107…
Comparing with 0.70884479192243 the result is not too bad.
The Reader can check L2, and L3 (I have already checked with Mathematica).
As this post became longer than I indented, and as there are things that I have to ponder about before next post, let us call it a day!





