Month: March 2017

Luminous eggs

Posted on by arkajad

“An incomplete person has a hole in the stomach,” she went on. “A sorcerer can see it as plainly as you can see my head. When the hole is on the left side of one’s stomach, the child who created that hole is of the same sex. If it is on the right side, the child is of the opposite sex. The hole on the left side is black, the one on the right is dark brown.”

“Can you see that hole in anyone who has had children?”

“Sure. There are two ways of seeing it. A sorcerer may see it in dreaming or by looking directly at a person. A sorcerer who sees has no problems in viewing the luminous being to find out if there is a hole in the luminosity of the body. But even if the sorcerer doesn’t know how to see, he can look and actually distinguish the darkness of the hole through the clothing.”
…..

“It’s very hard to tell,” she said after considerable coaxing. “She is the same as you and me, and yet she’s different. She has the same luminosity, but she’s not together with us. She goes in the opposite direction. Right now she’s more like you. Both of you have patches that look like lead. Mine is gone and I’m again a complete, luminous egg.

Carlos Castaneda, The second ring of power.

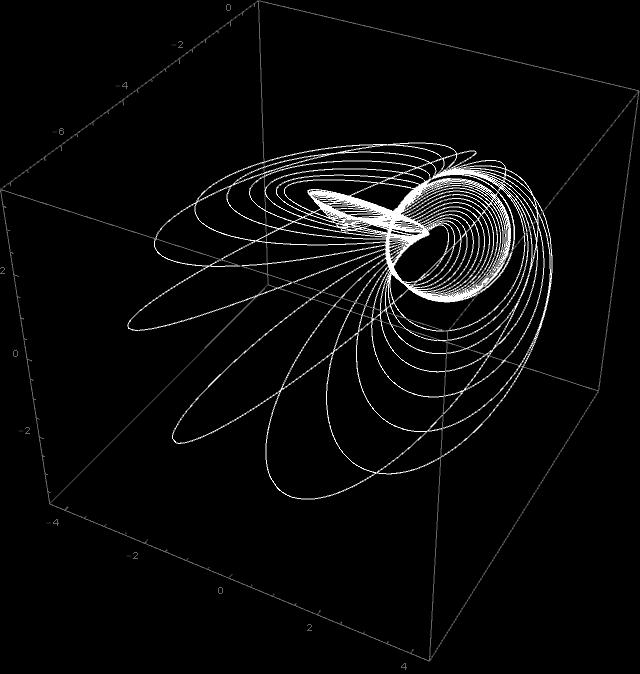
Today I was playing with trajectories for different values of d.
Below are trajectories for d=0.6, d=0.7 and d=0.8.
I was adjusting time (between 100 and 1000, and angle of view, so as to show
the interesting side of the figure.

Of course I could also rotate in dour dimensions. This would change the shape in 3D in a strange way.
So, here are the pictures:

d=0.6

d=0.7

d=0.8

Making these pictures is somewhat time consuming. Even with compiled functions the computer has to calculate Jacobi elliptic functions am, sd and pi for each point. And to make one trajectory I use 10 000 points, otherwise it may show bad zig-zags.

Probably I could do it faster writing a Fortran program, but writing such a program would take even more time.

Attitude matrix and quaternion path for m>1

Posted on by arkajad

I noticed that somehow I did not finish with the case m>1. So today, without further ado, I am posting the algorithm.
We have the body with I_1<I_2<I_3, and we are considering the case with d>1/I_2, where d is, as always, the ratio of the doubled kinetic energy to angular momentum squared.
Then we define

(1)   \begin{eqnarray*} A_1&=&\sqrt{\frac{I_1(dI_3-1)}{I_3-I_1}},\\ A_2&=&\sqrt{\frac{I_2 (1-dI_1)}{I_2-I_1}},\\ A_3&=&\sqrt{\frac{I_3 (1-dI_1)}{I_3-I_1}},\\ B&=&\sqrt{\frac{(dI_3-1)(I_2-I_1)}{I_1I_2I_3}},\\ \mu&=&\frac{1}{m}=\frac{(1-dI_1)(I_3-I_2)}{(dI_3-1)(I_2-I_1)}. \end{eqnarray*}

(2)   \begin{eqnarray*} L_1(t)&=&A_1\,\dn(Bt,\mu),\\ L_2(t)&=&A_2\,\sn(Bt,\mu),\\ L_3(t)&=&A_3\,\cn(Bt,\mu). \end{eqnarray*}

(3)   \begin{equation*} \alpha=\frac{I_3-I_1}{\sqrt{\frac{I_1(dI_3-1)(I_2-I_1)I_3}{I_2}}}, \end{equation*}

(4)   \begin{equation*} \nu=\frac{I_3-dI_1I_3}{I_1-dI_1I_3}. \end{equation*}

(5)   \begin{equation*} \psi(t)=\frac{t}I_3-\arctan\left((A_2/A_1)\mathrm{sd}(Bt,\mu) \right)+\alpha \Pi(\nu,\am(Bt,\mu),\mu),\ \end{equation*}

(6)   \begin{equation*} Q_1(t)=\begin{bmatrix}1-\frac{L_1(t)^2}{1+L_3(t)}&-\frac{L_1(t)L_2(t)}{1+L_3(t)}&-L_1(t)\\ -\frac{L_1(t)L_2(t)}{1+L_3(t)}&1-\frac{L_2(t)^2}{1+L_3(t)}&-L_2(t)\\L_1(t)&L_2(t)&L_3(t)\end{bmatrix}. \end{equation*}

(7)   \begin{equation*} Q_2(t)=\begin{bmatrix}\cos\psi(t)&-\sin\psi(t)&0\\\sin\psi(t)&\cos\psi(t)&0\\0&0&1 \end{bmatrix}. \end{equation*}

(8)   \begin{equation*} Q(t)=Q_2(t)Q_1(t). \end{equation*}

(9)   \begin{eqnarray*} q_0(t)&=&\sqrt{\frac{1+L_3(t)}{2}}\cos\frac{\psi(t)}{2},\\ q_1(t)&=&\frac{1}{\sqrt{2(1+L_3(t))}}\left(L_2(t)\cos\frac{\psi(t)}{2}+L_1(t)\sin\frac{\psi(t)}{2}\right),\\ q_2(t)&=&\frac{1}{\sqrt{2(1+L_3(t))}}\left(L_2(t)\sin\frac{\psi(t)}{2}-L_1(t)\cos\frac{\psi(t)}{2}\right),\\ q_3(t)&=&\sqrt{\frac{1+L_3(t)}{2}}\,\sin\frac{\psi(t)}{2},\\ q(t)&=&(q_0(t),q_1(t),q_2(t),q_3(t))=q_0(t)+\mathbf{i}\,q_1(t)+\mathbf{j}\,q_1(t)+\mathbf{k}\,q_3(t). \end{eqnarray*}

I use the above formulas to draw a stereographic projection of one particular path. So, I take I_1=1,I_2=2,I_3=3,d=0.5000001, and do the parametric plot of the curve \mathbf{r}(t) in \mathbf{R}^3,
with

    \[\mathbf{r}(t)=\left(\frac{q_1(t)}{1-q_0(t)},\frac{q_2(t)}{1-q_0(t)},\frac{q_3(t)}{1-q_0(t)}\right).\]

I show below two plots. One with t\in(-1000,1000), and one with t\in(-10000,10000). For this selected value of d, the time between consecutive flips, given by the formula

(10)   \begin{equation*}\tau =4\mathrm{EllipticK}(\mu)/B= 116.472.\end{equation*}

So, for t\in(-10000,10000) we have somewhat less than 200 flips, and the lines are getting rather densely packed in certain regions.
Notice that is just one geodesic line, geometrically speaking the straightest possible line in the geometry determined by the inertial properties of the body.

It is this “geometry”that will become the main subject of the future notes.

Geodesic line for t between -1000 and 1000

Geodesic line for t between -10000 and 10000

How can such a line be “straight”? Well, it is….

Zero in disguise

Posted on by arkajad

You look like an angel
Walk like an angel
Talk like an angel
But I got wise
You’re the zero in disguise
Oh, yes, you are
The zero in disguise

Elvis was singing about you ….

Ronan, in his recent comment under my post on Quaternion evolution, has noticed that Maple, the software he is using, gives for the function \psi(t) result that than the one I was advocating. How can it be? Mathematics is an exact science (physics, on the contrary, is not exactly an exact science). For a given question there should be one answer. Or is mathematics a devil in disguise? Looks like an exact science, walks like an exact science, but exact science it is not?

Devil likes to hide in the details, so let us examine the details.

My formula for \psi(t) comes from integration. I claim that if we integrate

(1)   \begin{equation*} \psi(t)=\int_0^t\frac{\cosh( \frac{s}{2\sqrt{3}})+1}{2\cosh(\frac{s}{2\sqrt{3}})+1}\,ds \end{equation*}

the result is given by rather simple a formula:

(2)   \begin{equation*} \psi_A(t)=\frac{t}{2}+ 2\arctan\left(\frac{\tanh \left(\frac{t}{4 \sqrt{3}}\right)}{\sqrt{3}}\right). \end{equation*}

Ronan, who is using Maple, gets for the same problem a different answer:

(3)   \begin{multline*} \psi_R(t)=\pi i \sqrt{3}+2\arctan(\frac{1}{3}\tanh(\frac{1}{12}t\sqrt{3})\sqrt{3})\\-\sqrt{3}\ln\left(\tanh\left(\frac{1}{12}t\sqrt{3}\right)-1\right)+\\\sqrt{3}\ln\left(\tanh\left(\frac{1}{12}t\sqrt{3}\right)+1\right). \end{multline*}

Taking the difference we get

(4)   \begin{multline*} \psi_A-\psi_R=\frac{t}{2}-\pi i\sqrt{3}+\\\sqrt{3}\ln\left(\tanh\left(\frac{1}{12}t\sqrt{3}\right)-1\right)-\sqrt{3}\ln\left(\tanh\left(\frac{1}{12}t\sqrt{3}\right)+1\right). \end{multline*}

If mathematics is not a devil in disguise, the last expression, namely \psi_A-\psi_R must be a zero in disguise. But is it?
I tried to ask Maple to simplify it, with no result. The algorithms known to otherwise very clever software are not smart enough. So, let is see what we can do with our eyes and hands.

The first thing that comes to our attention is that we have a difference of logarithms. And we know from the kindergarten that \ln a-\ln b=\ln\frac{a}{b}. So we write

(5)   \begin{equation*} \psi_A-\psi_R=\frac{t}{2}-\pi i\sqrt{3}+\sqrt{3}\ln\frac{\tanh\left(\frac{1}{12}t\sqrt{3}\right)-1}{\tanh\left(\frac{1}{12}t\sqrt{3}\right)+1}. \end{equation*}

But what is \tanh? We know that \tanh x=\sinh x/\cosh x, therefore

(6)   \begin{equation*} \frac{\tanh(x)-1}{\tanh(x)+1}=\frac{\frac{\sinh x}{\cosh x}-1}{\frac{\sinh x}{\cosh x}+1}=\frac{\sinh x -\cosh x}{\sinh x+\cosh x}. \end{equation*}

Now, \cosh x=(e^x+e^{-x})/2,\quad \sinh x=(e^x-e^{-x})/2, therefore \sinh x+\cosh x=e^x, \sinh x-\cosh x=-e^{-x}. Thus

    \[\frac{\tanh(x)-1}{\tanh(x)+1}=\frac{e^{-x}}{e^{x}}=-e^{-2x},\]

and so

    \[ \ln \frac{\tanh(x)+1}{\tanh(x)-1}=\ln -e^{-2x}.\]

We can write now

    \[\ln -e^{-2x}=\ln ((-1)e^{-2x})=\ln(-1)+\ln e^{-2x}=\ln(-1)-2x.\]

What is \ln(-1)? It is an imaginary number. We know that e^{\pi i}=-1, and if we ask Maple what is \ln(-1)? – the answer is i\pi. So, we finally get

    \[ \ln \frac{\tanh(x)+1}{\tanh(x)-1}= i\pi -2x.\]

In our case x=\frac{1}{12}t\sqrt{3}, 2x=\frac{1}{6}t\sqrt{3}.
In Eq. (5) we have \sqrt{3} in front of the \ln, so we get

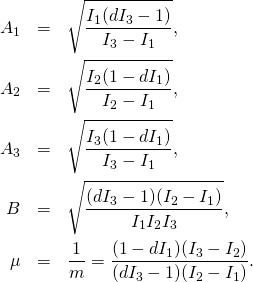
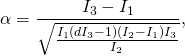
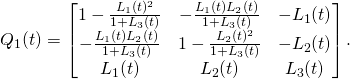
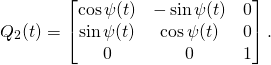
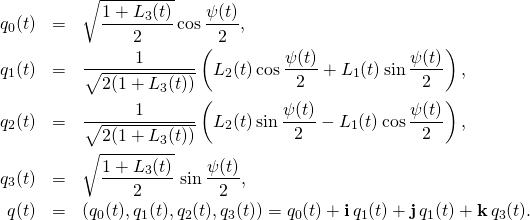
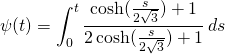
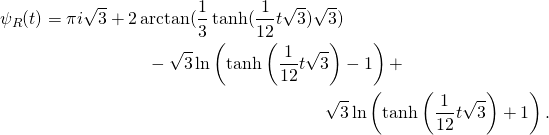
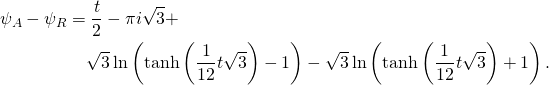
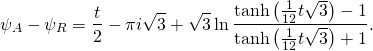
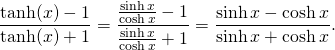
    \[\sqrt{3}\ln\frac{\tanh\left(\frac{1}{12}t\sqrt{3}\right)-1}{\tanh\left(\frac{1}{12}t\sqrt{3}\right)+1}=-\frac{t}{2}+\sqrt{3}i\pi. \]

Thus \psi_A-\psi_r=0. The zero has been cleverly disguised using functions \tanh and \ln. Einstein once commented that God is subtle, but He is not malicious. Well, here we could see Mathematics can be subtle