Day: April 10, 2017

The disk and the hyperbolic model

Posted on by arkajad

The unit disk in the complex plane, together with geometry defined by invariants of fractional linear SU(1,1) action, known as the Poincaré disk, that is the arena of hyperbolic geometry. But why “hyperbolic”? It is time for us to learn, and to use. In principle the answer is given in Wikipedia, under the subject “Poincaré disk model”. There we find the following picture

Poincare disk and hyperboloid

with formulas:

Transformation between hyperboloid and disk

We want to derive these formulas ourselves. Let us first introduce our private notation. The hyperboloid will live in a three-dimensional space with coordinates X,Y,T. This is the space-time of Special Relativity Theory, but in a baby version, with Z coordinate suppressed.

The light cone in our space-time has the equation T^2-X^2-Y^2=0. Of course we assume the constant speed of light c=1. Inside the future light cone (the part with Tgeq 0) there is the hyperboloid defined by T=\sqrt{1+X^2+Y^2}. The coordinates (X,Y,T) of events on this hyperboloid satisfy the equation

(1)   \begin{equation*}T^2-X^2-Y^2=1.\end{equation*}

As can be seen from the picture above, every straight line passing through the point with coordinates X_0=Y_0=0, T_0=-1 and a point with coordinates (X,Y,T) on the hyperboloid, intersects the unit disk at the plane T=0 at a point with coordinates (x,y). We want to find the relation between (X,Y,T) and (x,y).

Given any two points, P=(X_0,Y_0,T_0), Q=(X_1,Y_1,T_1), the points (X,Y,T) on the line joining P and Q have coordinates (X(u),Y(u),T(u)) parametrized by a real parameter u as follows:

(2)   \begin{equation*}(X(u),Y(u),T(u))=(1-u)(X_0,Y_0,T_0)+u(X_1,Y_1,T_1).\end{equation*}

For u=0 we are at P, for u=1 we are at Q, and for other values of u we are somewhere on the joining line. Our P has coordinates (0,0,-1), our Q has coordinates (X,Y,T) on the hyperboloid, and we are seeking the middle point with coordinate (x,y,0). So we need to solve equations

(3)   \begin{eqnarray*} x&=&(1-u)0+uX=uX,\\ y&=&(1-u)0+uY=uY,\\ 0&=&(1-u)(-1)+uT. \end{eqnarray*}

From the last equation we find immediately that u=1/(1+T), and the first two equations give us

(4)   \begin{eqnarray*} x&=&\frac{X}{1+T},\\ y&=&\frac{Y}{1+T}. \end{eqnarray*}

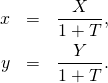
We need to find the inverse transformation. First we notice that

    \[x^2+y^2=\frac{X^2+Y^2}{(1+T)^2}=\frac{T^2-1}{(1+T)^2}=\frac{T-1}{T+1}.\]

Therefore 1-(x^2+y^2)=\frac{2}{T+1} and so

    \[T+1=\frac{2}{1-x^2-y^2},\]

    \[T=\frac{1+x^2+y^2}{1-x^2-y^2}.\]

Using Eqs. (4) we now finally get

(5)   \begin{eqnarray*} X&=&\frac{2x}{1-x^2-y^2},\\ Y&=&\frac{2y}{1-x^2-y^2},\\ T&=&\frac{1+x^2+y^2}{1-x^2-y^2}. \end{eqnarray*}

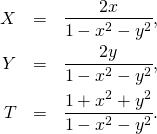
Thus we have derived the formulas used in Wikipedia. Wikipedia mentions also that the straight lines on the disk, that we were discussing in a couple of recent posts, are projections of sections of the hyperboloid by planes. We will not need this in the future. But we will use the derived formulas for obtaining the relation between SU(1,1) matrices and special Lorentz transformations of space-time events coordinates. This is the job for the devil of the algebra!