In the last post, SU(1,1) parametrization, we have concluded that the group SU(1,1) has the shape of a doughnut. Its elements can be uniquely parametrized by an angle ![]() and a complex number
and a complex number ![]() inside of the unit disk:
inside of the unit disk: ![]()

Thus SU(1,1) can be parametrized using the Cartesian product of the circle and the (interior of) the disk. But parametrization is one thing, and the actual construction is a different thing. Today we will see how every SU(1,1) matrix can be uniquely decomposed into a product of disk parametrized positive part, and circle parametrized unitary part.
We already know that every SU(1,1) matrix ![]() is of the form
is of the form
(1) ![]()
with
(2) ![]()
We also know (see Eqs. (11,14,15) from SU(1,1) parametrization) that it determines ![]() and
and ![]() so that
so that
(3) ![]()
(4) ![]()
(5) ![]()
Thus, writing it explicitly, ![]() is of the form:
is of the form:
(6) 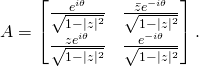
But then, as you can easily check, ![]() can be written as a product (so called polar decomposition)
can be written as a product (so called polar decomposition)
(7) ![]()
where
(8) 
(9) ![]()
with ![]() and
and ![]()
The matrix ![]() is evidently Hermitian:
is evidently Hermitian: ![]() It is also positive. Hermitian matrix is positive when all its eigenvalues are positive. In two dimensions there are two eigenvalues. Their product is the determinant, and so it is equal to 1. Thus either both eigenvalues are positive or both are negative. But the trace of
It is also positive. Hermitian matrix is positive when all its eigenvalues are positive. In two dimensions there are two eigenvalues. Their product is the determinant, and so it is equal to 1. Thus either both eigenvalues are positive or both are negative. But the trace of ![]() , which is the sum of eigenvalues, is positive
, which is the sum of eigenvalues, is positive ![]() is positive, therefore both eigenvalues must be positive, and so
is positive, therefore both eigenvalues must be positive, and so ![]() is positive.
is positive.
Exercise: calculate the two eigenvalues of ![]()
In fact every positive matrix from SU(1,1) is of the form ![]() for some
for some ![]() Since suppose
Since suppose ![]() is in SU(1,1) and is positive. We write it in the form as in Eq. (6). Positive matrix must be Hermitian, therefore
is in SU(1,1) and is positive. We write it in the form as in Eq. (6). Positive matrix must be Hermitian, therefore ![]() must be real. This happens only for
must be real. This happens only for ![]() or
or ![]() But
But ![]() so for
so for ![]() we would have
we would have ![]() which is impossible for a positive matrix. Therefore
which is impossible for a positive matrix. Therefore ![]() and
and ![]()
The matrix ![]() is evidently unitary,
is evidently unitary, ![]() In fact, every unitary matrix from SU(1,1) must be of the type
In fact, every unitary matrix from SU(1,1) must be of the type ![]() Why? Suppose
Why? Suppose ![]() in SU(1,1) is unitary. Write it in the form
in SU(1,1) is unitary. Write it in the form ![]() Suppose
Suppose ![]() Then
Then ![]() But
But ![]() is unitary and
is unitary and ![]() is Hermitian, so
is Hermitian, so ![]() Thus squares of the eigenvalues of
Thus squares of the eigenvalues of ![]() are both equal to
are both equal to ![]() and since
and since ![]() is positive, both must be equal to 1. Therefore
is positive, both must be equal to 1. Therefore ![]() and so
and so ![]()
Now, being familiar with the polar decomposition, we can fly, like these polar birds

and we will.