-
Recent Posts
- Kronecker generalized deltas and Levi-Civita epsilons 2026/01/09
- It’s all about permutations 2025/12/28
- Densities 2025/12/21
- Tensors on a picnic 2025/12/14
- Tensors are geometric objects 2025/12/10
- Conformal structure – until the puppy grows up 2025/12/07
- Growing Out of the Sandbox 2025/12/02
- Blog reincarnation with analytic idealism 2025/11/30
- Minkowski patches in the Einstein universe 2025/11/27
- Floating in the Einstein Universe 2025/11/24
- Comments on Clifford algebras 2019/01/24
- Comment on “Could ordinary quantum mechanics be just fine for all practical purposes?” by Alexey Nikulov 2018/03/08
- Spinning Top – Space Odity 2017/05/28
- Geodesics of left invariant metrics on matrix Lie groups – Part 2 Conservation laws 2017/05/26
- Geodesics of left invariant metrics on matrix Lie groups – Part 1 2017/05/24
- Killing vectors, geodesics, and Noether’s theorem 2017/05/23
- SL2R as anti de Sitter space cont. 2017/05/15
- Becoming anti de Sitter 2017/05/14
- SL(2,R) Killing vector fields in coordinates 2017/05/11
- Riemannian metrics – left, right and bi-invariant 2017/05/09
- Riemannian metric on SL(2,R)- explicit formula 2017/05/08
- Riemannian metric on SL(2,R) 2017/05/07
- Parametrization of SL(2,R) 2017/05/06
- Curvature of the upper half-plane 2017/05/05
- Geodesics on upper half-plane factory direct 2017/05/04
- Einstein the Stubborn 2017/05/03
- Dedekind tessellation on the Poincaré disk 2017/05/02
- Dedekind tessellation or circles all the way down 2017/04/30
- Real magic – space-time in Lie algebra 2017/04/29
- Geodesics on the upper half-plane – parametrization 2017/04/28
Recent Comments
Links
Posts
Categories
- AI
- Attitude matrix
- Compactified Minkowski space
- Conformal structure
- Dzhanibekov effect
- Elliptic functions
- Euler's equations
- General
- Geometry
- Hyperbolic geometry
- Linear Algebra
- Lorentz transforations
- Mathematica
- Moments of inertia
- Nauka (science)
- Nonlinear pendulum
- Philosophy
- Poinsot trajectories
- Quaternions
- Special relativity
- Spin and rotations
- Spin matrices
- Stereographic projection
- SU(1,1)
- Teoria względności szczególna
- Time (czas)
- Uncategorized
- Unconventional science
Archives
Open System – Ark's blog
Daily Archives: 2017/04/17
Recreations with Cayley transform
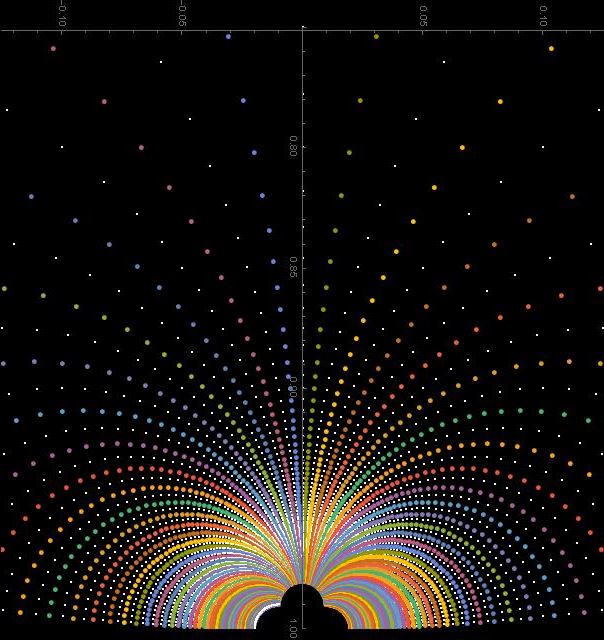
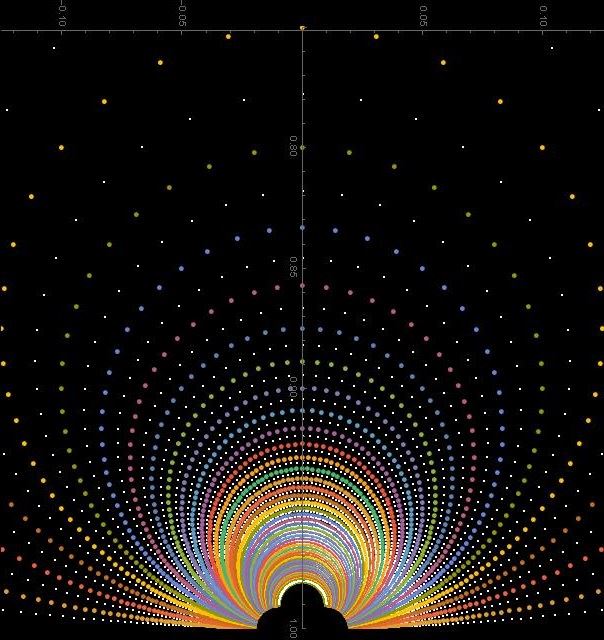
What can we do with Cayley transform? We can produce interesting pictures. Here are two such pictures: In fact in both pictures we have the same pattern of dots, but they are organized differently by coloring. How are these images … Continue reading
Posted in Geometry, Hyperbolic geometry, SU(1,1)
1 Comment
