As we have learned in SU(1,1) action on the disk, the matrix Lie group SU(1,1) acts transitively, by linear fractional transformations, on the unit disk ![]() in the complex plane. The disk
in the complex plane. The disk ![]() is a homogeneous space for SU(1,1). The points of the disk can be considered as orbits of the
is a homogeneous space for SU(1,1). The points of the disk can be considered as orbits of the ![]() subgroup of SU(1,1), acting on SU(1,1) from the right. In Getting hyperbolic we have already seen the actions of three one-parameter subgroups of SU(1,1), let us call them
subgroup of SU(1,1), acting on SU(1,1) from the right. In Getting hyperbolic we have already seen the actions of three one-parameter subgroups of SU(1,1), let us call them ![]() They come from exponentiation of three different generators
They come from exponentiation of three different generators ![]() elements of the Lie algebra of the group:
elements of the Lie algebra of the group:
(1) 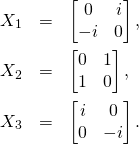
(2) 
Streamlines for these three one-parameter transformation groups (and they have been derived in Getting hyperbolic) acting on the disk are on the pictures below.
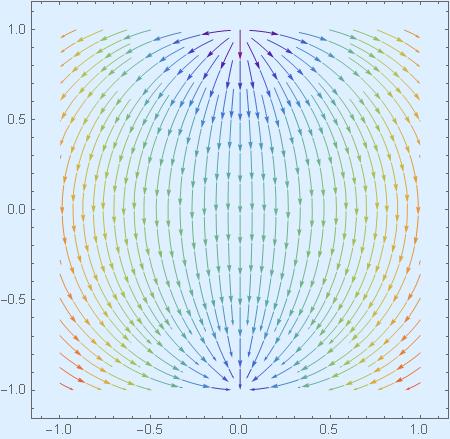

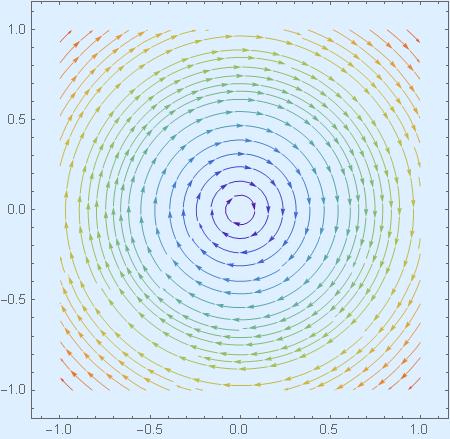
Now that we have transitive action of SU(1,1) on the disk, we can implement the Erlangen program and study disk’s geometry by analyzing properties of invariants of this action. We call SU(1,1) the symmetry group of the disk.
We will start with looking for a reasonable definition of “straight lines”. First let us consider the most reasonable candidate for a straight line of the disk’s geometry, the vertical line through the center ![]() of the disk:
of the disk:

Notice that it is the trajectory of ![]() that passes through the origin
that passes through the origin ![]()
It is a perfect candidate for a straight line. For when you start vertically, there is no reason to deflect to the right or to the left if you are going to move “straight”. Thus we take it as our primary straight line.
Of course arguing that “there is no reason to deflect” does not sound very rigorous. It is, I agree, a “baby talk“.

But in this case it is enough. I could have argued in a different way, in an “adult way“, by quoting from the second volume of Foundations of Differential Geometry by Kobayashi and Nomizu:

But the end result would be the same. The vertical line is a “geodesic”, is a “straight line”.
According to the Erlangen program for geometry, initiated by Felix, Klein, in our case we will call it “hyperbolic geometry” or “Lobachevsky-Bolyai geometry“, every transformation from the symmetry group transforms straight line into straight line. So, here I am using
![]() for
for ![]() going from -2, to +2, step 0.1, to get a family of 40 other straight lines of our geometry:
going from -2, to +2, step 0.1, to get a family of 40 other straight lines of our geometry:

They are all images of our vertical straight line. Therefore, even if they do not look very straight, they are, by definition.
But the one-parameter group ![]() is also a symmetry group of our geometry. Transformations from this group rotate around the center
is also a symmetry group of our geometry. Transformations from this group rotate around the center ![]() So rotations of our straight line are also straight lines. Here is a family of straight lines obtained from the horizontal line by applying the transformations
So rotations of our straight line are also straight lines. Here is a family of straight lines obtained from the horizontal line by applying the transformations ![]()

Notice that these straight lines are as long as they can only be, and they do not intersect. Therefore, by definition, they are all parallel.
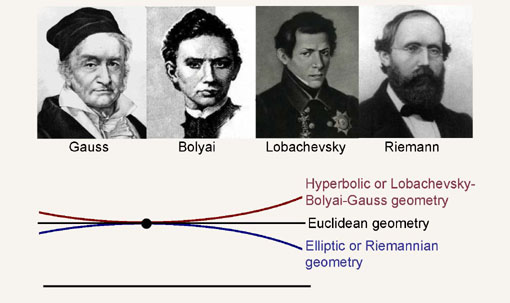
We will continue our adventure in the following posts. Once we are here, we must certainly touch the Fifth Euclid’s postulate – one that is violated in our geometry.




