We are going to solve now Euler’s equations. In order to solve them in an intelligent way we need some preparation.
In “Angular momentum” we have derived Euler’s equations that govern rotations of a free rigid body about its center of mass:
(Euler) 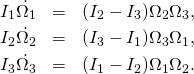
Here ![]() are the components of the angular velocity vector in the body frame, while
are the components of the angular velocity vector in the body frame, while ![]() are the three principal moments of inertia.
are the three principal moments of inertia.
Euler’s equations follow from conservation of the angular momentum vector with respect to space, as seen from the inertial laboratory frame. This is how we derived them in the previous post. The angular momentum vector in the laboratory frame is ![]() where
where ![]() has components
has components ![]() Although we do not know
Although we do not know ![]() (it needs to be found through solving differential equations), we know that it is an orthogonal matrix. And orthogonal matrix preserves the length of the vector. Since the components of the vector
(it needs to be found through solving differential equations), we know that it is an orthogonal matrix. And orthogonal matrix preserves the length of the vector. Since the components of the vector ![]() are constants, also its length is a constant. But the length of
are constants, also its length is a constant. But the length of ![]() is the same as the length of
is the same as the length of ![]() and the length squared
and the length squared ![]() of
of ![]() is
is
(1) ![]()
There is also another important constant of motion – kinetic energy. We denote by ![]() the doubled kinetic energy:
the doubled kinetic energy:
(2) ![]()
To see that indeed ![]() is a constant of motion, we differentiate
is a constant of motion, we differentiate ![]() with respect to
with respect to ![]() :
:
![]()
Now, we use the Euler’s equations and, surprise-surprise, everything on the right hand side cancels out:
(3) 
Thus we get ![]()
So, we have identified two important constants of motion. Whenever a rigid body rotates, it will change its orientation in space, its rotation axis may change its direction, but the absolute value ![]() of the angular momentum given by Eq. (1) is constant in time. Kinetic energy is also constant in time. Yet these two constants are not completely independent. There are restrictions on the possible values of
of the angular momentum given by Eq. (1) is constant in time. Kinetic energy is also constant in time. Yet these two constants are not completely independent. There are restrictions on the possible values of ![]() if
if ![]() is given. To see this let us order
is given. To see this let us order ![]() so that
so that
(4) ![]()
We then have:
![]()
For the same reason we have
![]()
Let us introduce the constant ![]() defined by
defined by
(5) ![]()
Then we have
(6) ![]()
We can now move to solving the Euler’s equations (Euler) – at the top. To this end we compare them with the properties of the derivatives of Jacobi elliptic functions ![]() that we have derived in “Derivatives of Jacobi elliptic am, sn, cn, dn“:
that we have derived in “Derivatives of Jacobi elliptic am, sn, cn, dn“:
(7) 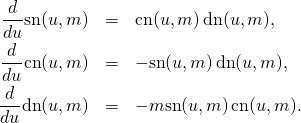
According to our convention (4) on the right hand side of Euler’s equation we have signs ![]() . Our guess is that
. Our guess is that ![]() is proportional to
is proportional to ![]() We do not know whether to assume
We do not know whether to assume ![]() proportional to
proportional to ![]() or to
or to ![]() ? Let us try
? Let us try ![]() proportional
proportional ![]() and
and ![]() proportional to
proportional to ![]() . So, here is our “Ansatz”:
. So, here is our “Ansatz”:
(8) 
Question is: can we find ![]() such that the Euler’s equation are satisfied automatically, given
such that the Euler’s equation are satisfied automatically, given ![]() and
and ![]() ?
?
The answer has been found long ago. We can see a solution in the 1894 book by Alfred Cardew Dixon, “The elementary properties of the elliptic functions” . But we want to do it in a modern way. Here, for instance, is REDUCE code that provides us with a solution:
o1(t):=A1*cn(B*t);
o2(t):=A2*sn(B*t);
o3(t):=A3*dn(B*t);
%To solve Euler’s equation we must have e1=e2=e3=0 where
e1:=(I1*DF(o1(t),t)-(I2-I3)*o2(t)*o3(t))/(dn(b*t)*sn(b*t));
e2:=(I2*DF(o2(t),t)-(I3-I1)*o3(t)*o1(t))/(cn(b*t)*dn(b*t));
e3:=(I3*DF(o3(t),t)-(I1-I2)*o1(t)*o2(t))/(sn(b*t)*cn(b*t));
% Here are properties of sn, cn, dn
For all v let DF(sn(v),v)=cn(v)*dn(v);
For all v let DF(cn(v),v)=-sn(v)*dn(v);
For all v let DF(dn(v),v)=-m*sn(v)*cn(v);
For all v let cn(v)**2=1-sn(v)**2;
For all v let dn(v)**2=1-m*sn(v)**2;
% en2 is twice kinetic energy:
en2:=I1*o1(t)^2+I2*o2(t)^2+I3*o3(t)^2;
% ll2 is square of angular momentum:
ll2:=I1^2*o1(t)^2+I2^2*o2(t)^2+I3^2*o3(t)^2;
OFF NAT;
OUT “H:\Reduce MyFiles\eu1.txt”;
e1;
e2;
e3;
% we use the three Euler’s equations in order to express A1,A2,A3 in terms of i1,i2,i3,b,m
xx:=solve({e1=0,e2=0,e3=0},{A1,A2,A3});
% We get four solutions, with different signs, we choose one with all signs plus:
PART(xx,3);
a1:= part(part(part(xx,3),1),2);
a2:= part(part(part(xx,3),2),2);
a3:= part(part(part(xx,3),3),2);
en2;
ll2;
% now we call angular momentum squared l^2 and we introduce d=en2/ll2.
% we then find m,b expressed through l and d
% again there are two solutions, with different signs. We choose both plus signs:
xxx:=solve({ll2=l^2,en2=l^2*d},{b,m});
b:=part(part(part(xxx,1),1),2);
m:=part(part(part(xxx,1),2),2);
% now we find final expressions for a1,a2,a3
a1:=a1;
a2:=a2;
a3:=a3;
SHUT “H:\Reduce MyFiles\eu1.txt”;
END;
The results spilled out by REDUCE are not yet nicely arranged. After the arrangement, taking into account our conventions, the answer takes the following form:
(9) 
Now I should verify that it is indeed a solution. I was trying to do it using REDUCE, but I did not succeed. So, I will return to this problem in my next post (and I will also try to fix typos in this post). Hopefully I will be able to find a way of verifying for sure the above statements.
Update: The following REDUCE code verifies the solution on random data. On output it spits out three zeros.:
a2:=l*sqrt((d*i3-1)/(I2*(i3-i2)));
a3:=l*sqrt((1-d*i1)/(i3*(i3-i1)));
b:=l*sqrt((1-d*i1)*(I3-i2)/(i1*i2*i3));
m:=(d*i3-1)*(i2-i1)/((1-d*i1)*(i3-i2));
o1(t):=A1*cn(B*t);
o2(t):=A2*sn(B*t);
o3(t):=A3*dn(B*t);
For all v let DF(sn(v),v)=cn(v)*dn(v);
For all v let DF(cn(v),v)=-sn(v)*dn(v);
For all v let DF(dn(v),v)=-m*sn(v)*cn(v);
For all v let cn(v)**2=1-sn(v)**2;
For all v let dn(v)**2=1-m*sn(v)**2;
e1:=(I1*DF(o1(t),t)-(I2-I3)*o2(t)*o3(t))/(dn(b*t)*sn(b*t));
e2:=(I2*DF(o2(t),t)-(I3-I1)*o3(t)*o1(t))/(cn(b*t)*dn(b*t));
e3:=(I3*DF(o3(t),t)-(I1-I2)*o1(t)*o2(t))/(sn(b*t)*cn(b*t));
for all a,b let sqrt(a)*sqrt(b)=sqrt(a*b);
off rounded;
i1:=random(1000)/1000;
i2:=1.0+random(1000)/1000;
i3:=2.0+random(1000)/1000;
l:=random(10)/2;
d:=1/i3+(1/i1-1/i3)/2;
OFF NAT;
OUT “H:\Reduce MyFiles\eu3.txt”;
e1:=e1;
e2:=e2;
e3:=e3;
SHUT “H:\Reduce MyFiles\eu3.txt”;
END;
Update 2:
Both REDUCE and Mathematica are able to do the task in a symbolic mode, but not without human help. These programs have very smart simplification algorithms, but sometimes our eye see that two expressions are the same, though they have different forms, while the programs do not want to see it. Then we need to help the program. For instance with Mathematica, it did not want to see that a particular expression is zero, but it recognized that its square is zero! Like here:

Here is the Mathematica notebook verifying Euler’s equations.
So, I consider that the job is done, and that we do have a solution of Euler’s equations.




“To see that indeed 2E is a constant of motion …”
2E is constant of motion – that’s proved.
But how do we know that E in (2) is kinetic energy?
In the sentence: “We denote by 2E the doubled kinetic energy: …”
the term “kinetic energy” is linked to a pdf file from MIT: Lecture L27 – 3D Rigid Body Dynamics: Kinetic Energy; Instability; Equations of Motion
The expression for the kinetic energy is derived there. Of course I could derive it here as well, but I thought the MIT file is sufficient?
Thanks for the Erratum!
“the term “kinetic energy” is linked to a pdf file…
The expression for the kinetic energy is derived there.”
There is something wrong with formula between formulas (2) and (3).
Perhaps it was clumsily written. I have fixed it, and also added the calculation.
I did not mean the formula between formulas (2) and (3) from this your post.
I meant formula between formulas (2) and (3) from MIT: Lecture L27 – 3D Rigid Body Dynamics
BTW, your new version of formula (3) lacks Omega factors.
@Bjab.
Indeed in MIT notes there is a missing left parenthesis.
Omegas added. Thanks.
Why did you input the Euler equations divided by Jacobi functions? I know when you simplify them all the Jacobi functions dissapear. The equations solve fine without them beig divided by the Jacobis’. Am I missing something here?
I magaged to get A1, A2, A3 & B and massage them into your form.
Software returns m as a square root of basicially what you have.
“Why did you input the Euler equations divided by Jacobi functions? I know when you simplify them all the Jacobi functions dissapear. ”
To separate the constants. It is not necessary indeed, but it makes my desktop cleaner.
“I magaged to get A1, A2, A3 & B and massage them into your form.
Software returns m as a square root of basicially what you have.”
Which software? I tried Reduce and Mathematica and both were not able to simplify certain expressions containing square roots. If you were able to do it – please share your code.
I use Maple 2016. I will try later this evening to post the code. The point/question was when I solved “solve({ll2=l^2,en2=l^2*d},{b,m})” in Maple m is given as the square root of what you have published.
I have only tried in Reduce what you posted above by copy and paste line by line. I don’t know Reduce at all.
Now no matter which version m or sqrt(m) is used the Euler equations simplify to zero.
Perahps Maple is smarter than Mathematica. If you post the code, I will try it. Perhaps I was underestimating Maple…. I know it is very good with Lie groups and differential geometry.
This is my code. I copy/pasted your Reduce code into Maple and edited it to suit. Couldn’t find a way to copy paste maple code here so also edit your Reduce code in Word to match.
Maple produced m as a complex/imaginary square root but that can be messaged out ok.
Maybe I have made a silly mistake in solving the last pair of equations but B comes out ok.
#We derive a solution of Euler’s equations
o1(t):=A1*cn(B*t|m);
o2(t):=A2*sn(B*t|m);
o3(t):=A3*dn(B*t|m);
#To solve Euler’s equation we must have e1=e2=e3=0 where
e1:=I1*DF(o1(t),t)-(I2-I3)*o2(t)*o3(t));
e2:=I2*DF(o2(t),t)-(I3-I1)*o3(t)*o1(t));
e3:=I3*DF(o3(t),t)-(I1-I2)*o1(t)*o2(t);
#en2 is twice kinetic energy:
en2:=I1*o1(t)^2+I2*o2(t)^2+I3*o3(t)^2;
# ll2 is square of angular momentum:
ll2:=I1^2*o1(t)^2+I2^2*o2(t)^2+I3^2*o3(t)^2;
% we use the three Euler’s equations in order to express A1,A2,A3 in terms of i1,i2,i3,b,m
xx:=solve({e1=0,e2=0,e3=0},{A1,A2,A3},explicit=true);
# We get 5 solutions, with different signs, we choose one with all the same signs in this case negative
a1:= simplify(rhs(xx[5,1]),symbolic);
a2:= simplify(rhs(xx[5,2]),symbolic);
a3:= simplify(rh2(xx[5,3]),symbolic);
en2a:=simplify(en2); #` Must do this simplify these else won’t solve`
ll2a:=simplify(ll2);
simplify(en2a/ll2a); # This cancels out B in can be solved on its own for m by setting = d
# now we call angular momentum squared l^2 and we introduce d=en2/ll2.
# we then find m,b expressed through l and d
# again there are two solutions, with different signs. We choose both plus signs:
xxx:=solve({ll2=L^2,en2=L^2*d},{b,m});
B:= simplify(rhs(xxx[1,1]),symbolic);
m:= simplify(rhs(xxx[1,2]),symbolic); #this is returned as a square root
# now we find final expressions for a1,a2,a3
a1;
a2;
a3;
B
m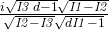
A1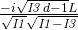
A2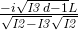
A3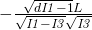
Thanks! Will try to use it. I was trying to do it all by myself from scratch, but got stuck when recalculating ll2 and en2 – it did not simplify correctlty. Perhaps with your tricks I will now succeed….
So, I modified your code. You will see how. It works ok! Here is what I got. Not too bad.
Now I am chasing errors/differances. The crux of the difference lies in e3. your equation contains m mine m^2.
In your simplification you have diff(dn(B t),t)=-m Bsn(B t)cn(b t)
Maple produces diff(dn(B t|m),t)=-m^2 B sn(B t|m)cn(B t|m).
Other differance you have dn(B t)^2=1-m sn(B t)^2, the m should be m^2
These 2 differances is why I am getting m as a square root
As a side question why do you use sn(B t) and then have to define it’s differential?
Maple is using the modulus m as the second argument of am,sn,cn,dn. I am using m=k^2 as the second argument (like in Matlab and in Mathematica).
Maple knows what is sn(z,k). It does not know what is sn(z). For Maple it is some “user function”. So I have to tell Maple what are properties of this function. The same with cn and dn. Maple knows that cn(z,k) is JacobiCN. But cn(z), with just one argument, is an abstract function. I could rely on Maple Jaacobi functions as well, but I have chosen not to.
Forgot to edit DF to diff
OK. I know about that.