For many years I was keeping my Polish blog. The discussions there were hot, it was rather normal to have over 100 of comments after each consecutive post. Now, that I have switched to English, everything instantly collapsed. Which was to be expected, nevertheless the collapse is a valid observation.
I am reading autobiography of Leopold Infeld, Polish theoretical physicist who worked with Albert Einstein. Wikipedia mentions that
“Infeld was one of the 11 signatories to the Russell–Einstein Manifesto in 1955, and is the only signatory never to receive a Nobel Prize.”
But that is not important here. What I want to point at is that Infeld was working with Einstein in Berlin, then in Princeton, then he had a position in Toronto. And yet in 1950 he returned to Poland. Why?

Infeld with Einstein
Reading his biography I am guessing that he was not among the best in Berlin, he was not among the best in Princeton, he was not the best, and no so important in Toronto. But after he has returned to Poland, he became important, the organizer of the Polish school of theoretical physics. He did a good and important job there.
I was “a somebody” on my Polish blog. There are not so many professors of theoretical physics that are blogging in Poland. Thus there were many readers, there were interesting contacts, correspondence, exchange of ideas, collaborations. But with my English blog I am nobody. There are thousands of similar blogs. The market is different. So far I have this luck that I have a dedicated collaborator who came from the Polish blog here. 99% of all discussion and stimulation comes from Him. Thank you Bjab!
This being said, let me finish handling the T-handle from the recent posts. What is still lacking is the case of ![]() that is
that is ![]() The point is that it is better to reduce everything to the case of
The point is that it is better to reduce everything to the case of ![]() since one should not rely on the implementation of Jacobi elliptic functions for
since one should not rely on the implementation of Jacobi elliptic functions for ![]() From my experience, Mathematica, for instance, can handle the case
From my experience, Mathematica, for instance, can handle the case ![]() but it is not always reliable. Fortunately we can reduce the case of
but it is not always reliable. Fortunately we can reduce the case of ![]() to that of
to that of ![]() and here is the complete algorithm:
and here is the complete algorithm:
Given
(1) ![]()
We recall the conversion formulas below
(2) ![]()
(3) ![]()
(4) ![]()
We arrive at the following algorithm:
(5) ![]()
(6) ![]()
(7) ![]()
(8) ![]()
(9) ![]()
(10) ![]()
(11) ![]()
(12) ![]()
(13) ![]()
(14) 
(15) 
(16) 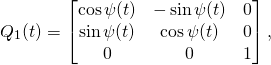
(17) ![]()
To get a general solution one may need to change the signs of two components from ![]() and/or shift the time:
and/or shift the time: ![]()





If it turns out better for you physics-wise to go back to a Polish blog, that’s zero problem for me. I followed your Polish blog via Google translate and I miss your comment sections from there too! (though there was that one guy there for a while kind of adding lots of spam comments).
I (like Ronan) am on the Cass forum so we can always find you there if needed too (I’ve done that before).
Did you have a reason for switching to hosting a blog in English? I was aware of you Polish Blog. For me this is great. I know I only appear to be part time on here. I am just about managing to keep up. All this level of maths is new, so I have to do a lot of background work. Youtube videos, finding articles that help etc. Fighting with Maple. I just have a home user license so don’t use it professionally. Spent hours over the past 10 days(nights) figuring how to animate a simple body. See http://www.mapleprimes.com/questions/221181-Animations-Not-Displaying (Haven’t figured out how to reduce the link to one word)
I know what I want to be able to show in the animation. Next I have to get to grips (and that will be a very loose grip) with you solution to the d(psi)/dt differential equation.
We the conversion formulas ->
?
Missing formula in the box for A_2
Shouldn’t be there 1/L in (14) ?
Thanks. Fixed. I decided to set L=1 here.
I decided to set L=1 here.”
Wouldn’t it be too inconsistent with (10),(11),(12) (which are not normalised I suppose).
In fact it is consistent. Using the formulas from the note we can calculate that
I supposed wrong.
So you did the calculations while I was doing them!
I had written about Infled (based on his autobiography) many years ago on the same polish blog vortal. :)