April 2000:  THE THIRD EXPEDITION

The ship came down from space. It came from the stars and the black velocities, and the shining movements, and the silent gulfs of space.
….
“Mars!” cried Navigator Lustig.
“Good old Mars!” said Samuel Hinkston, archaeologist.
“Well,” said Captain John Black.
The rocket landed on a lawn of green grass.
….
“I’ll be damned,” whispered Lustig, rubbing his face with his numb fingers. “I’ll be damned.”
“It just can’t be,” said Samuel Hinkston.

Ray Bradbury, The Martian Chroniques

And we are here on our third field expedition. During the first expedition we had seen the stream moving down:

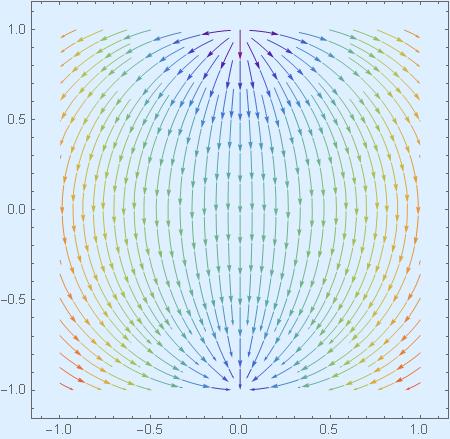
Then, in our second expedition the stream was flowing to the right.

What will happen in our third expedition? Will it flow up now? No. It will be something else. You will say “I’ll be damned, It just can’t be.” And yet here it is:

This time we take

The vector field comes as

Its plot is:

And the streamlines:

Oh, no, sorry, these are from Mars. Mathematica gives these:

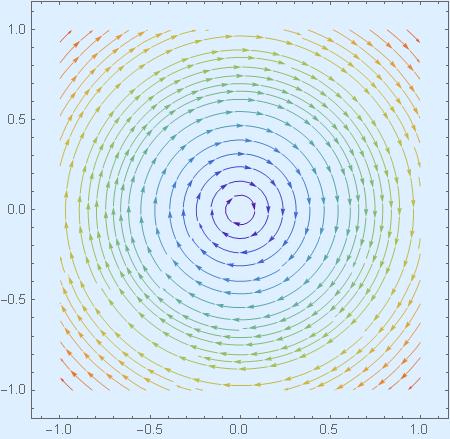
Now the mystery is this: Combining 1 and 2 one can get 3, combining 2 and 3 one can get 1, combining 3 and 1 one can get 2. Perhaps. It resonates, doesn’t it?

But how exactly this happens? Where are the details that devil dwells in?