“Standing on the shoulders of giants” was the title of my Polish blog post that was addressing the issue I need to address here and now, in my English blog.
From Wikipedia:
The metaphor of dwarfs standing on the shoulders of giants (Latin: nanos gigantum humeris insidentes) expresses the meaning of “discovering truth by building on previous discoveries”.[1] This concept has been traced to the 12th century, attributed to Bernard of Chartres. Its most familiar expression in English is by Isaac Newton in 1676: “If I have seen further, it is by standing on the shoulders of giants.”[2]
With us the story is that we also want to see further. But can we? Is that possible? Can a simple blog provide better information than original papers and monographs written by experts? To my own surprise I have found that yes, it can. Experts are human beings, they are always in a hurry, changing subjects of their research, making errors, leaving holes in arguments, and hoping that if there is someone really interested in the subject, then she/he will fix the errors, fill the holes, simplify the arguments, bring new observations.
Here is the image from Wikipedia:

And indeed we can provide additional pairs of eyes. My own adventure with the mechanics of flipping tops was possible because of several papers that I tried to study. I say “tried”, because I was not able to understand everything from these papers. Usually, after a year I have problems with understanding my own papers! But the paper that I really-really liked was this one:
Ramses van Zon, Jeremy Schofield, “Numerical implementation of the exact dynamics of free rigid bodies“, J. Comput. Phys. 225, 145-164 (2007)

In this paper the exact analytical solution of the motion of a rigid body with arbitrary mass distribution is derived in the absence of forces or torques. The resulting expressions are cast into a form where the dependence of the motion on initial conditions is explicit and the equations governing the orientation of the body involve only real numbers. Based on these results, an efficient method to calculate the location and orientation of the rigid body at arbitrary times is presented. This implementation can be used to verify the accuracy of numerical integration schemes for rigid bodies, to serve as a building block for event-driven discontinuous molecular dynamics simulations of general rigid bodies, and for constructing symplectic integrators for rigid body dynamics.
Then I also learned a couple of ideas from
Celledoni, Elena; Zanna, Antonella.E Celledoni, F Fassò, N Säfström, A Zanna, The exact computation of the free rigid body motion and its use in splitting methods, SIAM Journal on Scientific Computing 30 (4), 2084-2112 (2008)
Then I have found even more recent paper:
Marcello Romano, “Concise Form of the Dynamic and Kinematic Solutions of the Euler-Poinsot Problem“, Advances in the Astronautical Sciences Volume 145, (IAA-AAS-DyCoSS1-01-05), (2012)
It is this last paper that encouraged me to study the subject deeper. Romano, in particular, wrote:
It is a surprising fact that the exact solutions of the Euler-Poinsot problem are rarely taught in graduate courses of astrodynamics, or used in the engineering practice. It is even more surprising, in particular, that the kinematic solutions by Jacobi in terms of rotation matrix elements, as well as the associated remarkable geometric interpretation, are overlooked in the literature, and do not appear in any textbook of astrodynamics or celestial mechanics (to the best knowledge of the author). Two possible reasons of this fact are: the general lack of familiarity regarding the Jacobi elliptic and theta functions, and the inconvenient treatment of initial conditions and body geometry related to the usual formulation of the solutions (as given, for instance, limited to the dynamics, by Hughes and Wittenburg).
It is the goal of the author to foster, with the present paper, an increased familiarity, dissemination and utilization of the exact solutions of the Euler-Poinsot problem.
Well, well. For dissemination what can be better than the blog? So, here I am – disseminating! And doing it according to my own taste and feeling of what is simple and what is interesting.
Here we go, with the dissemination task. We are done with exact solutions of Euler’s equation for the free asymmetric top. But that is only half of the whole problem. We are dealing with mechanics or, better, dynamics. It was created by Newton and then, having particularly in mind rotating bodies, developed by Euler. The fundamental equation of dynamics is known from schools:
![]()
We have speed ![]()
![]()
and we have acceleration ![]()
![]()
To solve a mechanical problem we need to find ![]() , that is how position changes with time. Quite often we do it in two steps: we know the forces, so we know the acceleration. We integrate to find how velocity is changing with time. This is half of the work. But then we have to integrate again in order to find how position changes with time.
, that is how position changes with time. Quite often we do it in two steps: we know the forces, so we know the acceleration. We integrate to find how velocity is changing with time. This is half of the work. But then we have to integrate again in order to find how position changes with time.
With rotating bodies it is similar, except that instead of “velocity” we have “angular velocity”, and instead of “position” we have “orientation” (described by the “attitude matrix” ![]() ).
).

Employee Attitude Matrix
Employees can be divided into 4 groups using the employee commitment and employee satisfaction. They can be apostles, mercenaries, hostages and terrorists. The organisation should have a plan for all groups because they have different needs. They need to receive different messages from the leadership team.
:)
In previous posts we have learned how to solve Euler’s equations. They give us angular velocity ![]() in the body frame. But in order to find the orientation of the body with respect to the laboratory, we need to integrate the equation that relates the attitude matrix
in the body frame. But in order to find the orientation of the body with respect to the laboratory, we need to integrate the equation that relates the attitude matrix ![]() to
to ![]() Here I will rely on the content of the post Angular momentum. From Eq. (1) therein we have
Here I will rely on the content of the post Angular momentum. From Eq. (1) therein we have
(1) ![]()
where
![Rendered by QuickLaTeX.com \[W(t)=\begin{bmatrix}0&-\Omega_3(t)&\Omega_2(t)\\\Omega_3(t)&0&-\Omega_1(t)\\-\Omega_2(t)&\Omega_1(t)&0\end{bmatrix}=\begin{bmatrix}0&-\frac{L_3(t)}{I_3}&\frac{L_2(t)}{I_2}\\\frac{L_3(t)}{I_3}&0&-\frac{L_1(t)}{I_1}\\-\frac{L_2(t)}{I_2}&\frac{L_1(t)}{I_1}&0\end{bmatrix},\]](http://arkadiusz-jadczyk.eu/blog/wp-content/ql-cache/quicklatex.com-f959ab2cd60c6cd496f15ba98c6d3102_l3.png)
where we have used the relation between angular momentum and angular velocity:
![]()
![]() , the attitude matrix, is an orthogonal
, the attitude matrix, is an orthogonal ![]() real matrix. When we find it, we will know how the body rotates in space, as seen from the laboratory inertial frame. In order to find
real matrix. When we find it, we will know how the body rotates in space, as seen from the laboratory inertial frame. In order to find ![]() we need to solve the differential equation. In fact
we need to solve the differential equation. In fact ![]() is a matrix with
is a matrix with ![]() coefficients, so we need to solve a system of nine differential equations. From a general theory of differential equations (linear in our case) we know that if
coefficients, so we need to solve a system of nine differential equations. From a general theory of differential equations (linear in our case) we know that if ![]() is given at the initial time
is given at the initial time ![]() then the solution exists and is unique. This is encouraging but not very helpful. From the matrix form (1) we also see that if
then the solution exists and is unique. This is encouraging but not very helpful. From the matrix form (1) we also see that if ![]() is a solution, and if
is a solution, and if ![]() is a fixed orthonormal matrix, then
is a fixed orthonormal matrix, then ![]() is also a solution. It has very simple interpretation:
is also a solution. It has very simple interpretation: ![]() represents the motion with respect to a rotated laboratory, rotated by the rotation matrix
represents the motion with respect to a rotated laboratory, rotated by the rotation matrix ![]() Moreover, every solution
Moreover, every solution ![]() of our equation is of that form. Thus, if we find just one solution of our equation, then we know them all. But we need to find one. It is from the paper by van Zon and Schofield mentioned above that I learned the trick of how to simplify the task of solving nine differential equations. By using geometric reasoning it is possible to reduce the number of equations that need to be solved from nine to just one! It is quite possible that van Zone and Schofield learned the trick from someone else. That is what “standing on the shoulders of giants” means in practice. Albert Einstein was known for standing on the shoulders of others quite often, without quoting them explicitly. Apparently in his mind it is not important who does something, it is important what is being accomplished. I am not that original, I like to quote other people work, who were working in a similar direction, even if I am not using their results.
of our equation is of that form. Thus, if we find just one solution of our equation, then we know them all. But we need to find one. It is from the paper by van Zon and Schofield mentioned above that I learned the trick of how to simplify the task of solving nine differential equations. By using geometric reasoning it is possible to reduce the number of equations that need to be solved from nine to just one! It is quite possible that van Zone and Schofield learned the trick from someone else. That is what “standing on the shoulders of giants” means in practice. Albert Einstein was known for standing on the shoulders of others quite often, without quoting them explicitly. Apparently in his mind it is not important who does something, it is important what is being accomplished. I am not that original, I like to quote other people work, who were working in a similar direction, even if I am not using their results.
But let us return back to “what”, that is what the simplifying trick is about. We have reference frames, and we have angular momentum vector ![]() which is constant with respect to the laboratory frame (conservation of angular momentum). Therefore we can choose the laboratory frame so that
which is constant with respect to the laboratory frame (conservation of angular momentum). Therefore we can choose the laboratory frame so that ![]() has in this frame components
has in this frame components ![]() where
where ![]() is the length of
is the length of ![]() How to do it in practice?? We do not have to worry about it now, after all we are solving our equations in theory. When we are done with the theory, then we can return to the real world.
How to do it in practice?? We do not have to worry about it now, after all we are solving our equations in theory. When we are done with the theory, then we can return to the real world.
So, in the laboratory our vector ![]() has components
has components ![]() while in the rotating frame attached to the body it has components
while in the rotating frame attached to the body it has components ![]() Matrix
Matrix ![]() transforms components of vectors in the body frame into components of these vectors in laboratory. In particular it transforms
transforms components of vectors in the body frame into components of these vectors in laboratory. In particular it transforms ![]() into
into ![]() There are many orthogonal matrices that do just that. Suppose
There are many orthogonal matrices that do just that. Suppose ![]() and
and ![]() Then
Then
![]()
Therefore ![]() is an orthogonal matrix that keeps the vector
is an orthogonal matrix that keeps the vector ![]() fixed. It must be a rotation about the third axis. Therefore
fixed. It must be a rotation about the third axis. Therefore ![]() is of the form:
is of the form:
(2) 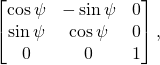
and ![]() Can we find easily some
Can we find easily some ![]() ? Yes, we can. And this is the trick:
? Yes, we can. And this is the trick:
(3) 
Here is simple REDUCE code verifying that ![]() is indeed orthogonal, and that
is indeed orthogonal, and that ![]() (even though checking it by hand is easy):
(even though checking it by hand is easy):
Lp:=sqrt(L1^2+L2^2);
L:=sqrt(L1^2+L2^2+L3^2);
Q:=mat(
(L1*L3/(L*Lp),L2*L3/(L*Lp),-Lp/L),
(-L2/Lp,L1/Lp,0),
(L1/L,L2/L,L3/L) );
Q*tp(Q);
Q*tp mat((L1,L2,L3))-tp mat((0,0,L));
END;
We have ![]() given as our solution of Euler’s equations. Therefore we know
given as our solution of Euler’s equations. Therefore we know ![]() It remains now to substitute
It remains now to substitute ![]() defined as
defined as
![Rendered by QuickLaTeX.com \[Q(t)=\begin{bmatrix}\cos\psi(t)&-\sin\psi(t)&0\\\sin\psi(t)&\cos\psi(t)&0\\0&0&1\end{bmatrix}\begin{bmatrix}\frac{L_1(t)L_3(t)}{LL_p(t)}&\frac{L_2(t)L_3(t)}{LL_p(t)}&-\frac{L_p(t)}{L}\\-\frac{L_2(t)}{L_p(t)}&\frac{L_1(t)}{L_p}&0\\\frac{L_1(t)}{L}&\frac{L_2(t)}{L}&\frac{L_3(t)}{L}\end{bmatrix},\quad L_p(t)=\sqrt{L_1(t)^2+L_2(t)^2},\]](http://arkadiusz-jadczyk.eu/blog/wp-content/ql-cache/quicklatex.com-3f4c09f40d1e284a379e4d5ca4e1130e_l3.png)
into Eq (1), find differential equation for ![]() , and solve it. It is an adventure. Standing on the shoulders of giants is always an adventure. What if one falls down from that height?
, and solve it. It is an adventure. Standing on the shoulders of giants is always an adventure. What if one falls down from that height?