“Ever present, never twice the same;
Ever changing, never less than whole”
~Robert Irwin
If for an instant he dozed off, the image of Fantômas took shape in his mind, but never twice the same: sometimes he saw a colossal figure with bestial face and muscular shoulders; sometimes a wan, thin creature, with strange and piercing eyes; sometimes a vague form, a phantom—Fantômas!
Marcel Allain, Pierre Souvestre, Fantomas
In the last post, Taming the T-handle continued, we have learned how to model free rotation of an asymmetric rigid body in that very-very special case when the ratio of the angular momentum squared to the kinetic energy doubled is exactly ![]() – the middle moment of inertia. In that case only one flip of the axis happens. For an infinite time, in the past, and in the future, the T-handle rotates along the
– the middle moment of inertia. In that case only one flip of the axis happens. For an infinite time, in the past, and in the future, the T-handle rotates along the ![]() axis, or rather: very close to this axis. In its whole infinitely long life only once it flips, in our case near
axis, or rather: very close to this axis. In its whole infinitely long life only once it flips, in our case near ![]() I say “near”, since what is, say
I say “near”, since what is, say ![]() , when compared with infinity?!
, when compared with infinity?!
Of course in practice we will never be able to achieve this particular ratio of angular momentum and kinetic energy exactly! But who cares? In practice there are no perfect straight lines and there are no perfect spheres. So what? When the ratio is “slightly” different, when the parameter ![]() that we used in all previous posts,
that we used in all previous posts, ![]() is “slightly” different from
is “slightly” different from ![]() , then the motion is quasi-periodic, though I am not sure if it is indeed quasi-periodic according to the mathematical definition of quasiperiodicity. From Wikipedia:
, then the motion is quasi-periodic, though I am not sure if it is indeed quasi-periodic according to the mathematical definition of quasiperiodicity. From Wikipedia:
In mathematics, a quasiperiodic function is a function that has a certain similarity to a periodic function. A function
is quasiperiodic with quasiperiod
if
where
is a “simpler” function than
. What it means to be “simpler” is vague.
In our case there are flips occurring periodically, the pattern repeats itself is a very similar way (though not exactly the same) again and again, the period can be calculated using elliptic ![]() -function. We have discussed it before, though we did not stress this phenomenon of “quasi” periodicity.
-function. We have discussed it before, though we did not stress this phenomenon of “quasi” periodicity.
In Taming the T-handle continued we have derived several important formulas. We have
(1) ![]()
where
(2) 
(3) 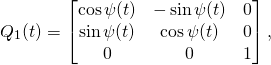
and ![]() (for
(for ![]() ) is given by:
) is given by:
![]()
![]() is periodic, with period
is periodic, with period ![]() But
But ![]() is not periodic at all. The functions
is not periodic at all. The functions ![]() and
and ![]() in
in ![]() are periodic, but
are periodic, but ![]() is a sum of two terms. The first term, linear in
is a sum of two terms. The first term, linear in ![]() , would make
, would make ![]() periodic. with period
periodic. with period ![]() , but the second term spoils any periodicity whatsoever. That is why the flips, though governed by the periodicity
, but the second term spoils any periodicity whatsoever. That is why the flips, though governed by the periodicity ![]() from the elliptic functions
from the elliptic functions ![]() never repeat exactly the same way.
never repeat exactly the same way.
Answers to Reader’s questions

In a comment to the last past Bjab formulated the following hypothesis:
So now there is a hypothesis that:
velocity of the end of the leg of T-handle is always perpendicular to the plane of T-handle.
Always means: when m=1
Proving (or disproving) this hypothesis is a good exercise. My T-handle is defined by the following Mathematica code:

In fact I have two slightly shifted T-handles, of different colors, so that it looks like one but painted top red, bottom yellow. The shift is in ![]() -direction, so that my T-handle is all in the plane
-direction, so that my T-handle is all in the plane ![]() The leg is along the
The leg is along the ![]() axis, from -0.9 to 0.2. We can assume that the leg end is at
axis, from -0.9 to 0.2. We can assume that the leg end is at ![]() The point
The point ![]() moves with time along the trajectory:
moves with time along the trajectory:
![Rendered by QuickLaTeX.com \[p(t)=Q(t)p_0.$ The velocity vector $\vec{v}$ at time $t$ is given by \[\vec{v(t)}=\frac{d}{dt}p(t)=\dot{Q}(t)p_0=Q(t)W(t)p_0.\]](http://arkadiusz-jadczyk.eu/blog/wp-content/ql-cache/quicklatex.com-d78c92830e1d64e0ee54802c015ca636_l3.png)
The plane of the T-handle is also rotated by the matrix ![]() therefore the angle between the velocity vector and the plane is the same as the angle between
therefore the angle between the velocity vector and the plane is the same as the angle between ![]() and the
and the ![]() plane. But
plane. But
![]() Thus
Thus ![]() has components
has components ![]() . This vector is orthogonal to
. This vector is orthogonal to ![]() but is at the angle
but is at the angle ![]() to
to ![]()
Therefore it seems that the hypothesis, though fruitful and interesting, should not be considered as proven.
Update: Why ![]() ? We know that
? We know that ![]() Thus
Thus ![]() We want to find the angle, so we are interested in normalized vector. Therefore we can skip the common
We want to find the angle, so we are interested in normalized vector. Therefore we can skip the common ![]() factor. Thus we see that the angle is constant in time – which is an interesting fact. In particular for
factor. Thus we see that the angle is constant in time – which is an interesting fact. In particular for ![]() we have
we have
![]()
The square root of the sum of squares is ![]() Therefore the normalized first component is
Therefore the normalized first component is ![]() We have
We have ![]()






