Many things in Nature are spinning. Perhaps the whole Universe is spinning. Perhaps spin is at the foundation of being. I like to ride my bicycle. Its wheels are spinning and I am moving forward, I am not falling down sideways. But then we learn that even elementary particles like electron, proton, neutron – they also have spin. But what is this spin? Nobody knows.
Or maybe they do know? Let’s check. We go to Scientific American site. There we find:
And not only they are asking this question that is bothering us, they also provide several answers from experts. But why several answers? If you ask experts they should all give the same answer, don’t they? I mean if they know. But perhaps they do not know? If they do not know, why they did not say so? Questions, questions, … Let us see the answers.
Morton Tavel, a professor of physics at Vassar College, responds:
“When certain elementary particles move through a magnetic field, they are deflected in a manner that suggests they have the properties of little magnets. In the classical world, a charged, spinning object has magnetic properties that are very much like those exhibited by these elementary particles. Physicists love analogies, so they described the elementary particles too in terms of their ‘spin.’
So, there is no real “spin”? It is just “analogy”? But if “spin” is just analogy, is there anything else in physics that is not just an analogy? Is there anything really real? But professor Morton Tavel did not finish yet. Here is the continuation:
“Unfortunately, the analogy breaks down, and we have come to realize that it is misleading to conjure up an image of the electron as a small spinning object. Instead we have learned simply to accept the observed fact that the electron is deflected by magnetic fields. If one insists on the image of a spinning object, then real paradoxes arise; unlike a tossed softball, for instance, the spin of an electron never changes, and it has only two possible orientations. In addition, the very notion that electrons and protons are solid ‘objects’ that can ‘rotate’ in space is itself difficult to sustain, given what we know about the rules of quantum mechanics. The term ‘spin,’ however, still remains.”
“So, the analogy is bad. We should not “conjure up an image of the electron as a small spinning object.” We have learned simply to accept … “We?” Who? All physicists? Or just “the majority”. Are there physicists who are not simply accepting? If one accepts, paradoxes arise. Come on, isn’t it paradoxical that people on other side of the planet are standing there upside down with respect to us? Paradoxes often arise because in our thinking we are making unspoken assumptions. ” The very notion that electrons and protons are solid ‘objects’ that can ‘rotate’ in space is itself difficult to sustain, given what we know about the rules of quantum mechanics.”. But do we understand quantum mechanics? Is everybody happy with it? Or there were and there are physicists who are very unhappy and would like to replace it by something better? Didn’t Feynman say that nobody understands quantum mechanics?
So, we did not learn much. But perhaps we will learn something in the next paragraph? Here it comes:
Kurt T. Bachmann of Birmingham-Southern College adds some historical background and other details:
“Starting in the 1920s, Otto Stern and Walther Gerlach of the University of Hamburg in Germany conducted a series of important atomic beam experiments. Knowing that all moving charges produce magnetic fields, they proposed to measure the magnetic fields produced by the electrons orbiting nuclei in atoms. Much to their surprise, however, the two physicists found that electrons themselves act as if they are spinning very rapidly, producing tiny magnetic fields independent of those from their orbital motions. Soon the terminology ‘spin’ was used to describe this apparent rotation of subatomic particles.
Here again we see “apparent rotation”. But is it only “apparent”? How do we know? The question was “What exactly is …”. But the answers are not really addressing this question. What about the next paragraph?
“Spin is a bizarre physical quantity. It is analogous to the spin of a planet in that it gives a particle angular momentum and a tiny magnetic field called a magnetic moment. Based on the known sizes of subatomic particles, however, the surfaces of charged particles would have to be moving faster than the speed of light in order to produce the measured magnetic moments. Furthermore, spin is quantized, meaning that only certain discrete spins are allowed. This situation creates all sorts of complications that make spin one of the more challenging aspects of quantum mechanics.”
Now we are learning something. Spin is bizzare. Perhaps something indeed rotates, but it would have to rotate faster than the speed of light, and that is a big no-no! Why? Because majority of physicists are not thinking, or they are thinking in a wrong way. There was a man who took his wife for a hat, and there are physicists who take religion for a science. Working on alternatives to Einstein’s relativity may cost a job, so it is better not to think too much.
But anyway we have learned that spin is one of the more challenging aspects of quantum mechanics. That’s something. Next is Victor J. Stenger, professor of physics at the University of Hawaii at Manoa, who offers another, more technical perspective:
“Spin is the total angular momentum, or intrinsic angular momentum, of a body. The spins of elementary particles are analogous to the spins of macroscopic bodies. In fact, the spin of a planet is the sum of the spins and the orbital angular momenta of all its elementary particles. So are the spins of other composite objects such as atoms, atomic nuclei and protons (which are made of quarks).
What are these quarks? And when do they get their spin from?
“In classical physics, angular momentum is a continuous variable. In quantum mechanics, angular momenta are discrete, quantized in units of Planck’s constant divided by 4 pi. Niels Bohr proposed that angular momentum is quantized in 1913 and used this to explain the line spectrum of hydrogen.
So, for some reason “quantum” angular momentum is quantized. But why?
“At our current level of understanding, the elementary particles are quarks, leptons (such as the electron) and bosons (such as the photon). These particles are all imagined as pointlike, so you might wonder how they can have spins. A simple answer might be, perhaps they are composite, too. But deep theoretical reasons having to do with the rotational symmetry of nature lead to the existence of spins for elementary objects and to their quantization. Of particular significance is the difference between fermions, particles that, like the electron, have half-integer spins (half-integer multiples of Planck’s constant divided by 2 pi), and bosons, particles that have integer spins. Fermions obey the Pauli exclusion principle, which states that two identical fermions cannot exist in the same state; without the Pauli exclusion principle, chemistry would have no Periodic Table. Bosons, on the other hand, tend to congregate in the same state, leading to phenomena such as superconductivity and Bose-Einstein condensation.
“These particles are all imagined as pointlike, so you might wonder how they can have spins.” Are imagined? By whom? By all, by some? By majority? “… you might wonder how they can have spins. A simple answer might be, perhaps they are composite, too.” How does it explain spin? Is everything composite? Who says so? Why?
“Spin has served as the prototype for other, even more abstract notions that seem to have the mathematical properties of angular momentum but do not have a simple classical analogue. For example, isotopic spin is used in nuclear physics to represent the two states of a ‘nucleon,’ the proton and neutron. Similarly, quarks are paired as isospin ‘up’ and ‘down,’ which are the names given to the two quarks that make up ordinary matter. The rotational symmetry of space and time is generalized to include symmetries in more abstract ‘inner’ dimensions, with the result that much of the complex structure of the microworld can be seen as resulting from symmetry breaking, connecting profoundly to ideas describing the spontaneous formation of structure in the macroworld.
This last paragraph has nothing to do with the original question. The real answer to this question is rather: We do not know, and there is a lot of work that needs to be done. But minds have to be kept open rather than closed.
There is a better answer in Quora, by Namit Anand, Budding physicist!Written Jul 22, 2016 Question: What is the physical interpretation of electron spin? It is worth checking. Towards the end we find there:
A final word:
Regarding the spin-1/2 , it comes from group theory and can’t be really explained well in a post; study some group theory for physicists and ask some more questions!
That’s all for today folks!
Group theory? Yes!!! That is what we are going to do now. It all has to do with rotations, and rotations do form a group. There is no point to avoid this fact, to hide it under the rug. Group theory is not a usual subject for elementary schools right now, but that can change soon, in about 1000 years. Group theory is common to both classical and quantum physics, so it may be the case that Nature has chosen group theory as one of her beloved instruments to play on.
What we need is the rotation group in three dimensions, so called special orthogonal group ![]() . From Wikipedia:
. From Wikipedia:
Consider the solid ball in
of radius
(that is, all points of
of distance
or less from the origin). Given the above, for every point in this ball there is a rotation, with axis through the point and the origin, and rotation angle equal to the distance of the point from the origin. The identity rotation corresponds to the point at the center of the ball. Rotation through angles between
and
correspond to the point on the same axis and distance from the origin but on the opposite side of the origin. The one remaining issue is that the two rotations through
and through
are the same. So we identify (or “glue together”) antipodal points on the surface of the ball. After this identification, we arrive at a topological space homeomorphic to the rotation group.
On the other hand ![]() is a group of matrices. It is the group of
is a group of matrices. It is the group of ![]() real orthogonal matrices of determinant
real orthogonal matrices of determinant ![]() How do we relate the picture above to the algebra of matrices? If we take a vector
How do we relate the picture above to the algebra of matrices? If we take a vector ![]() with length
with length ![]() , we can use it to build antisymmetric matrix
, we can use it to build antisymmetric matrix ![]() through the formula that we already know from previous posts (e.g. Angular momentum):
through the formula that we already know from previous posts (e.g. Angular momentum):
(1) 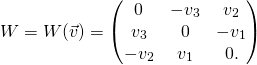
We can then take the matrix exponential:
![]()
We can write ![]() where
where ![]() is of unit length.
is of unit length.
Then we can use so called Rodrigues’ rotation formula
![]()
Notice that ![]() is antisymmetric:
is antisymmetric: ![]() and
and ![]() is symmetric. Therefore
is symmetric. Therefore
![]()
The matrix ![]() is automatically orthogonal, which can be checked in several ways. We will be playing with similar concepts for quite a while. The main idea is that the matrix
is automatically orthogonal, which can be checked in several ways. We will be playing with similar concepts for quite a while. The main idea is that the matrix ![]() that describes orientation of a rotating body is an orthogonal matrix that changes in time. Therefore it can be represented as a point within the unit ball on the picture above. The changing point makes a path. How such a path will look like? What is so particular about the trajectories of free rotating and flipping bodies in the rotation group? What is the difference between flipping and non-flipping histories? Perhaps there is some “gravity” there that is responsible for flips? We do not know, and we know that we do not know, because we do not understand spin. But we want to know. Lot of work….
that describes orientation of a rotating body is an orthogonal matrix that changes in time. Therefore it can be represented as a point within the unit ball on the picture above. The changing point makes a path. How such a path will look like? What is so particular about the trajectories of free rotating and flipping bodies in the rotation group? What is the difference between flipping and non-flipping histories? Perhaps there is some “gravity” there that is responsible for flips? We do not know, and we know that we do not know, because we do not understand spin. But we want to know. Lot of work….






