Day: February 1, 2017

Angular momentum

Posted on by arkajad

Let me start with recalling from Dzhanibekov effect – Part 4: The equations of motion.
We consider a free rigid body, observed from a laboratory that is an inertial reference system. The body is rotating with a fixed point at the center of its mass. The center of mass is at rest with respect to the laboratory.

Let \mathbf{E}_1(t), \mathbf{E}_2(t), \mathbf{E}_3(t) be an orthonormal frame corotating with the body, and aligned with its principal axes, and let \mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3 be an inertial laboratory frame, both centered at the center of mass of the body. The two frames are related by time-dependent orthogonal matrix A(t)

\mathbf{E}_i=A_{ji}\mathbf{e}_j,\quad X_i= A_{ij}x_j.

The inverse of A is denoted by Q

Q= A^{-1}=A^t,

and it is often called the attitude matrix. For a rotating body, if X_i are coordinates of a fixed point in the body, then its coordinates in the laboratory system change in time:
{\bf x}(t)=Q(t){\bf X}.

Differentiating we get

\frac{d{\bf x}(t)}{dt}=\frac{dQ(t)}{dt}{\bf X}=\frac{dQ}{dt}Q^{-1}(t)\,{\bf x}(t).

The matrix Q(t) is orthogonal, Q(t)Q(t)^t=I, therefore, by differentiating, the matrix \frac{dQ(t)}{dt}Q(t)^{-1} is antisymmetric. Every antisymmetric 3\times 3 matrix W can be written as

W = W({\bf v})=\begin{pmatrix}0& -v_3&v_2\\v_3&0&-v_1\\-v_2&v_1&0.\end{pmatrix}

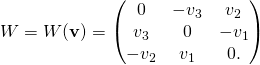
Writing \frac{dQ(t)}{dt}Q(t)^{-1}$ as $W(\boldsymbol{\omega}(t)):

(*)   \[ \frac{dQ(t)}{dt}Q(t)^{-1}=W(\boldsymbol{\omega}(t)),\]

we find that

\frac{d{\bf x}(t)}{dt}=\frac{dQ(t)}{dt}Q(t)^{-1}{\bf x}(t)=\boldsymbol{\omega}(t)\times{\bf x}(t).

Acting with the matrix W(\omega) is equivalent to taking the crossproduct with vector \omega.

The vector \boldsymbol{\omega}(t) is the angular velocity vector in the laboratory frame.

We denote by \boldsymbol{\Omega} the body representative of the angular velocity vector \boldsymbol{\omega}, where we skip the time dependence, with components \Omega_1,\Omega_2,\Omega_3.
Thus

\boldsymbol{\omega}= Q \boldsymbol{\Omega},

(**)   \begin{equation*} W(\boldsymbol{\omega})=QW(\boldsymbol{\Omega})Q^t.\end{equation*}

In a comment to this post Bjab asked: why (**)? Where is it coming from?
Good question. We have the relation

    \[W(\Omega)\mathbf{v}=\Omega\times\mathbf{v}\]

for any vectors \Omega and \mathbf{v}. If Q is a rotation matrix with determinant 1, then it follows from the definition of the cross product (see e.g. Rotational invariance of cross product) that

    \[ Q\Omega\times Q\mathbf{v}=Q(\Omega\times\mathbf{v}). \]

Therefore

    \[W(Q\Omega)Q\mathbf{v}=QW(\Omega)\mathbf{v}.\]

Let us set Q\mathbf{v}=\mathbf{w},\, \mathbf{v}=Q^t\mathbf{v}. then

    \[W(Q\Omega)\mathbf{w}=QW(\Omega)Q^t\mathbf{w}.\]

Since \mathbf{w} can be arbitrary, we get

    \[W(Q\Omega)=QW(\Omega)Q^t.\]

Now, from Eq. (*)

(1)   \begin{equation*} W(\boldsymbol{\Omega})=Q^t\dot{Q},\end{equation*}

where \dot{Q}=dQ(t)/dt. In the body frame the inertia tensor I is diagonal I=\mathrm{diag}(I_1,I_2,I_3). The angular momentum vector \mathbf{L} in the body frame is then given by the formula

\mathbf{L}=I\boldsymbol{\Omega},
or

    \[L_1=I_1\Omega_1,\,L_2=I_2\Omega_2,\,L_3=I_3\Omega_3.\]

The definition of the angular momentum \mathbf{L} is thus similar to the definition of the linear momentum. Liner momentum \mathbf{p} is the product of mass m and velocity \mathbf{v}. Angular momentum, in the body frame, \mathbf{L} is a vector whose components are products of moments of inertia I_i and angular velocity components \omega_i. The expression for the angular momentum in the body frame is very simple, but the law of conservation of the angular momentum refers to angular momentum vector in the laboratory frame. The transition from the body to the laboratory frame is implemented by the attitude matrix Q. Therefore what is conserved is Q\mathbf{L}:

(2)   \begin{equation*}\frac{d}{dt} \left(Q(t)\mathbf{L}(t)\right)=0.\end{equation*}

From this we get:

    \[ \dot{Q}(t)\mathbf{L}(t)+Q(t)\frac{d}{dt}\mathbf{L}(t)=0.\label{eq:c2}\]

From Eq. (1) we have that \dot{Q}=QW(\boldsymbol{\Omega}), therefore Eq. (??) reduces to

    \[ Q(t)W(\boldsymbol{\Omega})\mathbf{L}(t)+Q(t)\frac{d}{dt}\mathbf{L}(t)=0.\label{eq:c2a}\]

or, multiplying by Q(t)^{-1} from the left:

    \[ W(\boldsymbol{\Omega})\mathbf{L}(t)+\frac{d}{dt}\mathbf{L}(t)=0.\label{eq:c2a}.\]

But W(\boldsymbol{\Omega})\mathbf{L}=\boldsymbol{\Omega}\times\mathbf{L}=-\mathbf{L}\times\boldsymbol{\Omega},
therefore

    \[ \frac{d}{dt}\mathbf{L}(t)=\mathbf{L}\times\boldsymbol{\Omega}.\label{eq:c2b}.\]

Using the definition \mathbf{L}=(I_1\Omega_1,I_2\Omega_2,I_3\Omega_3), we arrive at

(Euler) 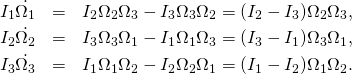  \begin{eqnarray*}I_1\dot{\Omega_1}&=&I_2\Omega_2\Omega_3-I_3\Omega_3\Omega_2=(I_2-I_3)\Omega_2\Omega_3,\\ I_2\dot{\Omega_2}&=&I_3\Omega_3\Omega_1-I_1\Omega_1\Omega_3=(I_3-I_1)\Omega_3\Omega_1,\\ I_3\dot{\Omega_3}&=&I_1\Omega_1\Omega_2-I_2\Omega_2\Omega_1=(I_1-I_2)\Omega_1\Omega_2. \end{eqnarray*}

These are the famous Euler’s equations. At the end of Dzhanibekov effect – Part 4: The equations of motion they were written in terms of (L_1,L_2,L_3), Here they are written in terms of \Omega_1,\Omega_2,\Omega_3.

We need to solve them. But first we will look at them with a magnifying glass. In the next couple of posts.