We will start with a simple road. Like that in Nebraska in the last post,

except that we take a nice blue sky with some puffy clouds:

Instead of T-handle (as in Taming the T-handle ) we take the nice, asymmetric, but as much symmetric as possible, spinning top, with principal moments of inertia ![]()
The x-axis, with the smallest moment of inertia, is along the two bronze spheres. The y-axis, with the middle moment of inertia, is along blue-red line. The z-axis, whose moment of inertia is the sum of the other two, is vertical.
The vertical z-axis is the natural axis to try to spin the thing. Imagine our top is floating in space, in zero gravity. We take the z-axis between our fingers, and spin the device. If our hand is not shaking too much, our top will nicely spin about the z-axis. This is the most stable axis for spinning.
The corresponding solution of Euler’s equation is ![]() where
where ![]() is a constant. The solution of the attitude matrix equation is
is a constant. The solution of the attitude matrix equation is ![]()
The square of angular momentum vector is ![]() the doubled kinetic energy is
the doubled kinetic energy is ![]() the parameter
the parameter ![]() that we were using in the previous notes is
that we were using in the previous notes is ![]() The parameter
The parameter ![]() is just zero,
is just zero, ![]() In what follows for simplicity we will take
In what follows for simplicity we will take ![]()
We will start with describing the spin history in ![]() using stereographic projection described in Chiromancy in the rotation group.
using stereographic projection described in Chiromancy in the rotation group.
In fact, we already did it in Dzhanibekov effect – Part 1, and Dzhanibekov effect – Part 2, but that was at the very beginning of this series, and we did not know yet what we were doing! So, now we do it again, in a more “legal” way.
Rotation about an axis ![]() by an angle
by an angle ![]() can be described by (see Eq. (4) in Putting a spin on mistakes) an
can be described by (see Eq. (4) in Putting a spin on mistakes) an ![]() matrix:
matrix:
(1) ![]()
In fact in Putting a spin on mistakes I have made a mistake that I corrected only at this moment, when checking it again: I have forgotten the imaginary ![]() in the formula!
in the formula!
We will be rotating about the z-axis, so we take ![]() Then
Then ![]() Therefore
Therefore
(2) ![]()
Comparing with Eq. (1) in Chiromancy in the rotation group, we get
(3) 
The stereographic projection (Eq. (4) in Chiromancy in the rotation group ) is
(4) 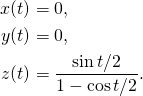
We can use trigonometric formulas to simplify:
(5) ![]()
Here is the plot of ![]() from
from ![]() to
to ![]() :
:
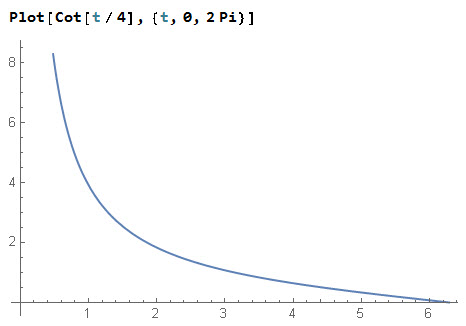
At ![]() we have
we have ![]() That is OK, because at
That is OK, because at ![]() the frame of the body coincides with the laboratory frame. The rotation
the frame of the body coincides with the laboratory frame. The rotation ![]() is the identity, its stereographic image is at infinity.
is the identity, its stereographic image is at infinity.
At ![]() we get
we get ![]() That is the point representing the matrix
That is the point representing the matrix ![]() It also describes the identity rotation in
It also describes the identity rotation in ![]() We get a straight path, the positive part of the z-axis. It is like the road in Nebraska at the top.
We get a straight path, the positive part of the z-axis. It is like the road in Nebraska at the top.

In the next posts we will learn how to travel more dangerous, less traveled roads.




