Day: February 7, 2017

More is different

Posted on by arkajad

We all know that more is different. Don’t we? But listen to Philip Anderson, who in 1977 was awarded the Nobel Prize in Physics for his investigations into the electronic structure of magnetic and disordered systems, which allowed for the development of electronic switching and memory devices in computers. He ends his paper “More is different” in Science journal as follows

The arrogance of the particle physicist and his intensive research may be behind us (the discoverer of the positron said “the rest is chemistry”), but we have yet to recover from that of some molecular biologists, who seem determined to try to reduce everything about the human organism to “only” chemistry, from the common cold and all mental disease to the religious instinct. Surely there are more levels of organization between human ethology and DNA than there are between DNA and quantum electrodynamics, and each level can require a whole new conceptual structure.
In closing, I offer two examples from economics of what I hope to have said. Marx said that quantitative differences become qualitative ones, but a dialogue in Paris in the 1920’s sums it up even more clearly:

FITZGERALD: The rich are different from us.
HEMINGWAY: Yes, they have more money.

Things are not simple, they are complex, sometimes very hard to understand. We need skills and tricks, intelligence and luck, we need to find our creative muse, which is not an easy task, and even with all that, understanding complexity is often a very complex task.

Now, here we are, with our asymmetric spinning top – the hardest concept in all physics – and there are questions that we need to answer. Like for instance the question asked by Bjab in a comment to the last post Crack in the Cosmic egg:

“But another question is interesting?
Can white point move along a curve in the northern hemisphere in the opposite direction?”

To which I replied (without any explanation whatsoever)

“Interesting question. Yes and no. But why yes and why no? Not so trivial.”

We need to answer those questions that can be answered. Then we will see in full light those questions that are still without answers. So, let’s do it. More is different, so now I go for more.

  1. Angular velocity vector 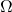\vector{\Omega} of our free asymmetric top, in the body frame, satisfies Euler’s equations

    (Euler)   \begin{eqnarray*}I_1\dot{\Omega_1}&=&(I_2-I_3)\Omega_2\Omega_3,\\ I_2\dot{\Omega_2}&=&(I_3-I_1)\Omega_3\Omega_1,\\ I_3\dot{\Omega_3}&=&(I_1-I_2)\Omega_1\Omega_2. \end{eqnarray*}

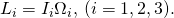    From the very structure of Euler’s equations we see that if the three components of \vector{\Omega}, (\Omega_1(t),\Omega_2(t),\Omega_3(t)), satisfy Euler’s equations, and we change the sign of any two of them, then we will have another solution of Euler’s equations. The same concerns angular momentum components L_i=I_i\Omega_i,\,(i=1,2,3). That is because either both of these changed components are on the right, then the product of two minuses cancels out giving plus, or one is on the left and one is on the right, and again the changes cancel out.
    Now, changing two components of a vector is equivalent to 180 degrees rotation about the third axis.

  2. Let us have a look at the first animation from the previous post:

    Here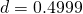 d=0.4999 and the code for the solution has these lines:

    A1 = Sqrt[I1*(d*I3 – 1)/(I3 – I1)];
    A2 = Sqrt[I2*(d*I3 – 1)/(I3 – I2)];
    A3 = Sqrt[I3*(1 – d*I1)/(I3 – I1)];
    m = ((d*I3 – 1)*(I2 – I1))/((1 – d*I1)*(I3 – I2))
    m1[t_] = A1*JacobiCN[B*t, m];
    m2[t_] = A2*JacobiSN[B*t, m];
    m3[t_] = A3*JacobiDN[B*t, m];

    The vertical axis on the animation is the third axis. 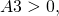A3>0, and the function 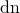\dn is always non-negative. That is why the point moves in the northern hemisphere. If we change the signs of the first two components of the angular momentum vector, that is equaivalent to the rotation by 180 degrees around the vertical axis. The motion will be the same, but the point will be on the opposite side of the curve.

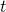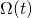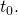  3. Euler’s equations concern \vector{\Omega}(t), whose components are functions of time, but the equations do not contain time t explicitly. Therefore if \vector{\Omega}(t) is a solution, then \vector{\Omega}(t+t_0) is another solution, for any t_0. We can move the origin of the time axis to any point in time. Let us have a look at the table from Periods of Jacobi elliptic functions – Part 1:

    We see that time translation by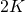 2K is the same as changing the signs of the first two components. And this is the same as shifting the point on the trajectory by half of its period, which is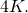 4K.

  4. Changing the sign of components (1,3) or (2,3) takes us to the trajectory on the southern hemisphere. The function 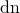\dn is non-negative, so 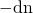-\dn is non-positive.
  5. Let us look now at the second animation, for d=0.5001.

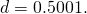
    Now the parameter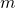 m is larger than 1: 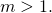m>1. One has to be careful now, because the definitions of the Jacobi functions for 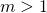m>1 are tricky (see The case of inverted modulus – Treading on Tiger’s tail and Jacobi elliptic cn and dn):

    (1)   \begin{equation*}\mathrm{cn}(u,m)=\mathrm{dn}(ku,1/m),\quad m>1\end{equation*}

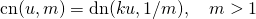
    (2)   \begin{equation*}\mathrm{sn}(u,m)=\frac{1}{k}\mathrm{sn}(ku,1/m)\quad m>1\end{equation*}

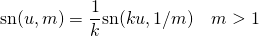
    (3)   \begin{equation*}\mathrm{dn}(u,m)=\mathrm{cn}(ku,\frac{1}{m}),\quad m>1.\end{equation*}

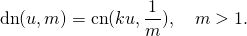
    Now it is the first component (that contains 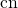\cn, that is \dn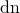) that is always non-negative. That’s why the trajectory is on the right. If we change the signs of 1 and 2 (or 1 and 3) components, we can move to the trajectory on the left etc.

  6. But we never go on the same trajectory in the opposite direction. Why? This morning I received an email from one of the readers. He notices the fact that the angular velocity and angular momentum vectors are, in fact, pseudovectors, and they are “abstract constructs describing reality.” And indeed. Angular momentum, by its very nature is a “bivector”, not a vector. We represent it as vector using a certain convention. And we draw it using certain conventions. In Angular momentum we have seen this piece:

    … matrix W can be written as

    W = W({\bf v})=\begin{pmatrix}0& -v_3&v_2\\v_3&0&-v_1\\-v_2&v_1&0.\end{pmatrix}

    .

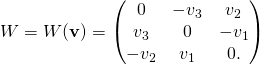
    Why this way? Why not opposite signs? And then, why to draw in a right-handed coordinate system? We can’t represent a bivector as a vector without using some conventions about what is right and what is left. And in more than 3 dimensions vectors and bivectors belong to completely different species!

    I know it is getting complex…. But so is life.