I am reading Leopold Infeld, “QUEST: The Evolution of a Scientist“, Readers Union Limited, London 1942. There is a little piece there about errors that drew my attention. The story takes place in Princeton:
The next day I met Robertson in Fine Hall and told him :
” I am convinced now that gravitational waves do not exist. I believe I am able to show it in a very brief way.” Robertson was still sceptical :
” I don’t believe you,” and he suggested a more detailed discussion. He took the two pages on which I had written my proof and read it through.
“The idea is O.K. There must be some trivial mistake in your calculations.”
He began quickly and efficiently to check all the steps of my argument, even the most simple ones, comparing the results on the blackboard with those in my notes. The beginning checked beautifully. I marvelled at the quickness and sureness with which Robertson performed all the computations. Then, near the end, there was a small discrepancy. He got plus where I got minus. We checked and rechecked the
point; Robertson was right. At one place I had made a most trivial mistake, in spite of having repeated the calculations three times ! Such a mistake must have as simple an explanation as a Freudian slip in writing or language. Subconsciously I did not believe in the result and my first doubts were still there. But I wanted to prove it in a simpler way than had Einstein. Thus I had to cheat myself. Such mistakes happen often, but they are usually caught before papers are printed. The author comes back. many times to his work. before he sees it. in print and has, therefore, plenty of opportunity to gain a more detached attitude and to apply the criteria of logic which were repressed during the emotional strain of creation.
Thus my whole result went to pieces. Although it was a very small matter, I felt very downcast at the moment, as does every scientist in similar circumstances even though he has accustomed himself to disappointment. He feels the collapse of hope, the death of the creation of his brain. It is like the succession of birth and death.
Robertson tried to console me :
” It happens to everyone. The most trivial mistakes are always most difficult to detect.”
Interesting! But who is this Robertson?
From Wikipedia:
Howard Percy “Bob” Robertson (January 27, 1903 – August 26, 1961) was an American mathematician and physicist known for contributions related to physical cosmology and the uncertainty principle. He was Professor of Mathematical Physics at the California Institute of Technology and Princeton University.
…
After the war Robertson was director of the Weapons System Evaluation Group in the Office of the Secretary of Defense from 1950 to 1952, chairman of the Robertson Panel on UFO’s in 1953 and Scientific Advisor to the NATO Supreme Allied Commander Europe (SACEUR) in 1954 and 1955. He was Chairman of the Defense Science Board from 1956 to 1961, and a member of the President’s Science Advisory Committee (PSAC) from 1957 to 1961.
… The Robertson Panel recommended that a public education campaign should be undertaken in order to reduce public interest in the subject, minimising the risk of swamping Air Defence systems with reports at critical times, and that civilian UFO groups should be monitored.
….
A number of criticisms have been leveled at the Robertson panel. In particular that the panel’s study of the phenomena was relatively perfunctory and its conclusions largely predetermined by the earlier CIA review of the UFO situation.
…Robertson Panel was a device used by the CIA to establish a cover program (Blue Book) that would draw attention away from a covert program designed to meet the UFO challenge.
Richard M. Dolan, Jacques F. Vallee,
UFOs and the National Security State: Chronology of a Coverup, 1941-1973, Hampton Roads 2002
So, it seems that H. P. Robertson knew not only how to avoid mistakes, but he also knew how to mislead others.
As for me, I am very good in the mistakes making business. My ideas are most of the time correct, but when it comes to their implementation, I am making a lot of mistakes. At every step. That is probably because I am impatient. So, when I want to get some result, I am going as quickly as I can to the end – just to see that the method is working, even if the end result is wrong. And the method is working if it produces result, because there are many methods that lead to no result at all. And when I have a method that is producing results, then I start working on removing mistakes. Usually I check the end result using several different methods. It is rather improbable that the same mistake will show up when you use different methods.
But then when I have everything working, I need to write it down, in all details. And that is pain. That is where I am making more mistakes.
Why is it so? It must be something more than the lack of patience. It is not a Freudian slip, I am sure, though sometimes it may be the case….
Anyway it is time now to go back to calculations, where making mistakes is so easy.

Let me recall from the previous post Pauli, rotations and quaternions.
We consider the group ![]() of complex
of complex ![]() unitary matrices of determinant 1. We have Hermitian traceless matrices
unitary matrices of determinant 1. We have Hermitian traceless matrices ![]() given by Eq. (1) in Pauli, rotations and quaternions. To each vector
given by Eq. (1) in Pauli, rotations and quaternions. To each vector ![]() we associate Hermitian matrix
we associate Hermitian matrix
![]() as in Eq. (10) in the previous post. We have orthogonal transformation
as in Eq. (10) in the previous post. We have orthogonal transformation ![]() defined by
defined by
![]()
We know that ![]() is orthogonal. We would like to know that
is orthogonal. We would like to know that ![]() and that is where we left in the last note.
and that is where we left in the last note.
One way of proving that ![]() has determinant 1 is to express
has determinant 1 is to express ![]() in terms of the elements of the matrix
in terms of the elements of the matrix ![]() We know (see the previous post) that
We know (see the previous post) that ![]() has the form
has the form
(1) ![]()
where ![]() It is now a straightforward calculation to express
It is now a straightforward calculation to express ![]() in terms of
in terms of ![]() and
and ![]() . But the calculation is long, and it is easy to make a mistake. That is why I used REDUCE , an excellent free computer algebra software (and then double checked with Mathematica). The REDUCE file doing the calculation is here. And here is the end result:
. But the calculation is long, and it is easy to make a mistake. That is why I used REDUCE , an excellent free computer algebra software (and then double checked with Mathematica). The REDUCE file doing the calculation is here. And here is the end result:
(2) 
Or in terms of quaternionic components ![]() as in Eq. (9) of the previous post:
as in Eq. (9) of the previous post:
(3) 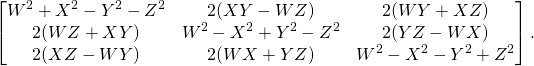
The REDUCE file producing the above matrix is here.
Then I used REDUCE again to verify that ![]() defined as above is indeed unitary and has determinant one. The REDUCE file is here here.
defined as above is indeed unitary and has determinant one. The REDUCE file is here here.
It takes a while to write the code and to debug it, but then producing the result is almost instant.
There is one more property that we need to verify. We have the map ![]() that maps
that maps ![]() matrices into orthogonal matrices of determinant 1. But we would like to be sure that every rotation
matrices into orthogonal matrices of determinant 1. But we would like to be sure that every rotation ![]() can be obtained in this way. How to do it? One way would be to calculate
can be obtained in this way. How to do it? One way would be to calculate ![]() and
and ![]() from the matrix
from the matrix ![]() using the formulas above. But that would not be easy. We have four real numbers and nine quadratic equations. There is a smarter and more useful method. Here is how we do it: suppose that we know that every rotation
using the formulas above. But that would not be easy. We have four real numbers and nine quadratic equations. There is a smarter and more useful method. Here is how we do it: suppose that we know that every rotation ![]() that is every orthogonal matrix of determinant 1, is a rotation about some axis by some angle (and it is true). That is we can represent
that is every orthogonal matrix of determinant 1, is a rotation about some axis by some angle (and it is true). That is we can represent ![]() as
as
![]()
where ![]() is a unit vector. That was discussed in the note Spin – we know that we do not know.
is a unit vector. That was discussed in the note Spin – we know that we do not know.
From the Rodrigues rotation formula discussed in this note we can calculate ![]() explicitly.
explicitly.
On the other hand we can calculate explicitly ![]() and then
and then ![]() It is then the question of a straightforward calculation to verify that we get our
It is then the question of a straightforward calculation to verify that we get our ![]()
(4) ![]()
The calculation is simple but long. REDUCE code that does it is here.






